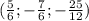Пошаговое объяснение:
Выразим из 2-го уравнения :
Подставим в 1-е:
Откуда
Откуда для единственности x;y;a получаем, что
Тогда
То есть у системы единственное решение возможно при
и это
Пошаговое объяснение:
Выразим из 2-го уравнения :
:
Подставим в 1-е:
Откуда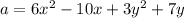
Откуда для единственности x;y;a получаем, что
Тогда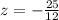
То есть у системы единственное решение возможно при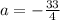
и это