Выделяем полные квадраты:
для x:
9(x²-2·3x + 3²) -9·3² = 9(x1-3)²-81
для y:
-16(y²+2·21 + 2²) +16·2² = -16(y1+2)²+64
В итоге получаем:
9(x-3)²-16(y+2)² = 144
Разделим все выражение на 144
(9(x-3)²/144) - (16(y+2)²/144) = 144/144,
((x-3)²/16) - ((y+2)²/9) = 1,
Данное уравнение определяет гиперболу ((x-3)²/4²) - ((y+2)²/3²) = 1
с центром в точке C(3; -2) и полуосями: a = 4 (действительная полуось); b = 3 (мнимая полуось).
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами с учётом центра (3; -2).
Определим параметр c: c² = a² + b² = 16 + 9 = 25.
c = 5.
Координаты фокусов (3 +-5; -2) = (-2; -2) и (8; -2).
Тогда эксцентриситет будет равен: е = с/а = 5/4.
Асимптотами гиперболы будут прямые: у + уо = ±(b/a)(x - xo).
y = ±(3/4)(x - 3) + 2.
Краткое решение ниже, вот подробные пояснения по поводу каждого шага.
Для начала переведем километры в метры, чтобы было проще считать.
км = м => км = м - работа
Теперь, исходя из данных о скоростях обеих бригад, вычислим скорость второй.
Скорость первой бригады = м/день
Скорость второй бригады = м/день = м/день
Общая скорость = скорость 1 + скорость 2, следовательно:
Скорость, если обе бригады будут работать вместе: м/день
Теперь вспомним формулу нахождения работы, через нее выразим формулу нахождения времени при данной работе и скорости.
, где - работа, - скорость, - время.
Подставим данные в формулу.
дней уйдет на асфальтирование дороги.
ответ: дней.
Если решать задачу по действиям (краткое решение):
1) м/день - скорость второй бригады.
2) день - общая скорость бригад, если они будут работать вместе.
3) дней - затраченное время.
Выделяем полные квадраты:
для x:
9(x²-2·3x + 3²) -9·3² = 9(x1-3)²-81
для y:
-16(y²+2·21 + 2²) +16·2² = -16(y1+2)²+64
В итоге получаем:
9(x-3)²-16(y+2)² = 144
Разделим все выражение на 144
(9(x-3)²/144) - (16(y+2)²/144) = 144/144,
((x-3)²/16) - ((y+2)²/9) = 1,
Данное уравнение определяет гиперболу ((x-3)²/4²) - ((y+2)²/3²) = 1
с центром в точке C(3; -2) и полуосями: a = 4 (действительная полуось); b = 3 (мнимая полуось).
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами с учётом центра (3; -2).
Определим параметр c: c² = a² + b² = 16 + 9 = 25.
c = 5.
Координаты фокусов (3 +-5; -2) = (-2; -2) и (8; -2).
Тогда эксцентриситет будет равен: е = с/а = 5/4.
Асимптотами гиперболы будут прямые: у + уо = ±(b/a)(x - xo).
y = ±(3/4)(x - 3) + 2.
Краткое решение ниже, вот подробные пояснения по поводу каждого шага.
Для начала переведем километры в метры, чтобы было проще считать.
Теперь, исходя из данных о скоростях обеих бригад, вычислим скорость второй.
Скорость первой бригады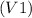 =
= 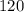 м/день
м/день
Скорость второй бригады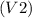 =
= 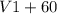 м/день =
м/день = 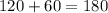 м/день
м/день
Общая скорость = скорость 1 + скорость 2, следовательно:
Скорость, если обе бригады будут работать вместе: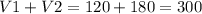 м/день
м/день
Теперь вспомним формулу нахождения работы, через нее выразим формулу нахождения времени при данной работе и скорости.
Подставим данные в формулу.
ответ: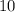 дней.
дней.
Если решать задачу по действиям (краткое решение):
1)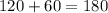 м/день - скорость второй бригады.
м/день - скорость второй бригады.
2)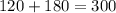 день - общая скорость бригад, если они будут работать вместе.
день - общая скорость бригад, если они будут работать вместе.
3)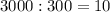 дней - затраченное время.
дней - затраченное время.
ответ: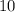 дней.
дней.