4. Даны четыре точки А0;7:1), B(4;1;5), C(4;6;3),
D3,9;8). Определите: а) объем пирамиды
ABCD, 0) длину высоты, опущенной из вершины D на плоскость грани ABC, и уравнение
соответствующей ей прямой; в) угол между ребром AD и медианой треугольника ABC,
проведенной из вершины Аг) уравнение плоскости, проходящей через точку D параллельно
плоскости ABC.

4. Даны четыре точки А0;7:1), B(4;1;5), C(4;6;3), D3,9;8). Определите: а) объем пирамиды ABCD, 0) дл

Показать ответ

Ответ:

gulia2369

28.03.2020 21:12

На вложенном рисунке диагональные сечения пирамиды с введенными обозначениями:

P - середина AM

O - центр основания, она же основание высоты

Q - проекция P на основание

L - пересечение высоты пирамиды и CP

K и N - точки пересечения ребер MD и MB плоскостью сечения (по условию эта прямая параллельна BD).

Теперь рассмотрим длины некоторых отрезков:

|AC| = |BD| =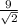 $\frac{9}{\sqrt{2}}$

Из подобия треугольников APQ и AMO

$|AQ| = \frac{|AO|}{2} = \frac{|AC|}{4} = \frac{9\sqrt{2}}{8}$

$|MO|= \sqrt{12^2-(\frac{9\sqrt{2}}{4})^2}}=\sqrt{\frac{1071}{8}}=3\sqrt{\frac{119}{8}}$

Достаточно очевидно, что

$\frac{|QC|}{|OC|} = \frac{3}{2}$

из подобия треугольников CPQ и CLO имеем:

$\frac{|PQ|}{|LO|} = \frac{QC}{OC} = \frac{3}{2}$

следовательно:

$|LO| = \frac{2}{3}|PQ| = \frac{2}{3}(\frac{1}{2}|MO|) = \frac{|MO|}{3} = \sqrt{\frac{119}{8}}$

Из подобия треугольников MDB и MKN:

$|KN| = \frac{|ML|}{|MO|}|DB| = \frac{2}{3}|DB| = \frac{9\sqrt{2}}{3}$

$|PC| = \sqrt{|PQ|^2+|QC|^2} = \sqrt{\frac{9*119}{4*8}+\frac{9*81}{16*2}} =\\ = \sqrt{\frac{900}{16}}=\frac{15}{2}$

Вполне очевидно, что BD перпендикулярно плоскости ACM

Следовательно и KN перпендикулярно ей, а значит и прямой PC

А т.к. диагонали четырехугольника CKPN перпендикулярны, то его площадь равна произведению длин этих диагоналей...

$S = |PC|*|KN| = \frac{15}{2}*\frac{9\sqrt{2}}{3}=\frac{45\sqrt{2}}{2}\approx 31.82$

Вправильной четырех-угольной пирамиде mabcd c вершиной m стороны основания равны 9/2, а боковые ребр

0,0(0 оценок)

Ответ:

oilga03

07.02.2023 18:56

первое число 7, тогда пусть третье число это х, значит второе это 7х
т.е ряд будет такой 7 7х х
тогда 4е число будет 1/7, 5е будет 1/(7х) (подбираем так, чтобы каждое число было произведением двух соседних)
т.е ряд будет такой 7 7х х 1/7 1/(7х) 1/х 7 7х х
Заметим, что седьмое число такое же, как и первое, и соответственно следующие за ним
То есть числа будут повторяться с периодичностью 6
то есть (1+6n) число будет равно 7, где n=0,1,2,3...16
(2+6n) будет равно 7х и так далее
последнее число будет при n=16, т.е 6*16+4. И оно будет равно четвертому числу то есть 1/7