4. На координатной плоскости постройте квадрат KLMN с вершинами в точках: К(- 3;0); L(1;6); М(7;2); N(3;-4).
а) Найдите координаты точки 0- пересечения диагоналей КМ и LN.
б) Найти координаты точки пересечения луча смс осями координат ​

Нет

Пошаговое объяснение:

Допустим, что число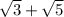 рационально, тогда при возведении в квадрат оно останется рациональным. 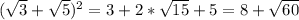, так как 8 целое, то 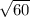рациональное. Пусть оно равно 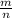, где m - целое, n - натуральное, а дробь несократима. Тогда 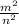= 60, так как 60 делится на 3, то 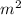делится на 3, значит m делится на 3, а 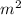делится на 9, но так как 60 не делится на 9, то 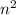делится на 3, а значит n делится на 3, значит дробь сократима - противоречие, тогда  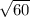не является рациональным числом, значит 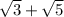тоже не является рациональным числом

11/(sqrt(37)*sqrt(58)).

Пошаговое объяснение

Обозначим O - точка пересечения медиан AK и CL.

1.) Запишем теорему косинусов для треугольника ABK:

AK^2=AB^2+BK^2-2*AB*BK*cos(45)

AK^2=(3sqrt(2))^2+(5/2)^2-2*3sqrt(2)*(5/2)*(sqrt(2)/2)= 37/4 => AK=sqrt(37)/2

Поскольку медианы точкой пересечения делятся в отношении 2:1, считая от вершины, OK=1/3*AK=sqrt(37)/6.

2.) Аналогично находим LC и OC.

Теорема косинусов для треугольника BLC:

LC^2=BL^2+BC^2-2*BL*Bc*cos(45) = 29/2 => CL=sqrt(29/2)

При этом OC=(2/3)*CL=sqrt(58)/3 (медианы точкой пересечения делятся в отношении 2:1, считая от вершины).

3.) Запишем теорему косинусов для треугольника СOK:

KC^2=OK^2+OC^2-2*OK*OC*cos(KOC)

Подставляя все найденное в это уравнение, находим cos:

сos(KOC)=11/(sqrt(37)*sqrt(58)) - искомый косинус. Угол же между медианами равен arccos(11/(sqrt(37)*sqrt(58))).