Пошаговое объяснение:
для обоих случаев:
Площадь криволинейной трапеции - это определенный интеграл для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
1)
f(x) = 6x -6x²; y=0; x=0; x=1
(-2x³) Ι₀¹ + 3x²Ι₀¹ = -2 +3 = 1
точки для построения графика
х=0; у= 0;
х= 0,2; у=0.96
х= 0,4; у = 1,44
х=0,6; у=1,44
х=0,8; у = 0,96
х = 1; у= 0
2)
f(x) = х³ - 1; y=0; x=2; x=3
(х⁴/4) Ι₂³ + (-х) Ι₂³ = 65/4 -1 = 61/4
х=2; у=7
х=2,2; у = 9,65
х = 2,4; у=14,62
х=2,6; у=16,58
х=2,8; у=20,95
х=3; у=26
Графики на фото.
файл 11 - график f(x) = 6x -6x²; y=0; x=0; x=1
файл 22 - график f(x) = х³ - 1; y=0; x=2; x=3
Пошаговое объяснение:
для обоих случаев:
Площадь криволинейной трапеции - это определенный интеграл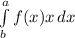
для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
1)
f(x) = 6x -6x²; y=0; x=0; x=1
(-2x³) Ι₀¹ + 3x²Ι₀¹ = -2 +3 = 1
точки для построения графика
х=0; у= 0;
х= 0,2; у=0.96
х= 0,4; у = 1,44
х=0,6; у=1,44
х=0,8; у = 0,96
х = 1; у= 0
2)
f(x) = х³ - 1; y=0; x=2; x=3
(х⁴/4) Ι₂³ + (-х) Ι₂³ = 65/4 -1 = 61/4
точки для построения графика
х=2; у=7
х=2,2; у = 9,65
х = 2,4; у=14,62
х=2,6; у=16,58
х=2,8; у=20,95
х=3; у=26
Графики на фото.
файл 11 - график f(x) = 6x -6x²; y=0; x=0; x=1
файл 22 - график f(x) = х³ - 1; y=0; x=2; x=3
1) 2 1/3 < x/3 < 2/3 ⇔7/3<x/3 < 2/3 ⇔7<x< 2
2) 1 5/12 < 17/x < 2 1/8 ⇔17/12<17/x < 17/8 ⇔ 17/12<17/x
{ ⇔
17/x < 17/8
+ - +
1/12<1/x (x-12)/(12)x<0 0 12
{ ⇔ { ⇔ + - +
1/x < 1/8 (x-8)/(8x)>0 -08
x∈(8;12)