4. УМНОЖЕНИЕ ДВУЗНАЧНОГО ЧИСЛА НА ДВУЗНАЧНОЕ
Пусть требуется вычислить произведение 34 • 29. Заменим второй
множитель 29 суммой разрядных слагаемых 20 и 9. Получим
Используя правило умножения числа на сумму, получим
34 • 29 = 34 - (20 +9) = 34 - 20 + 34 - 9 = 680 + 306 = 986.
Эти вычисления удобно выполнять письменно. Запишем числа 34
(ПИСЬМЕННЫЕ ВЫЧИСЛЕНИЯ)
34 - (20 + 9).
и 29 в столбик одно под другим.
5.
6
1
Найдём первое неполное
произведение:
умножим 34 на 9. Получим 306.
3.
Х
29
30 6.
68
986
неполное
+
2 Найдём Второе
произведение:
умножим 34 на 20. Для этого достаточно
умножить 34 на 2 и к полученному произве-
дению
Но
приписать нуль.
ЭТОТ нуль Мы
приписывать не будем, оставим его место свободным,
неполное произведение 68 дес. (или 680) начнём подписывать
под десятками.
3 Найдём сумму двух неполных произведений. Сложим числа
306 и 680 и получим число 986.
а второе
ответ. 986.
1. Выполни умножение с объяснением(в столбик).
19. 46
27. 35
42 • 23
25. 25
1. В основании призмы лежат - многоугольники.
2. Боковые рёбра призмы - перпендикулярны основаниям.
3. Призма имеет 30 граней. В её основании лежит (какой многоугольник) - многоугольник в 28 углов, 84 рёбер, 56 вершин.
(Боковых граней 30-2=28. Значит это 28-угольник. Вершины = 28×2, рёбра = 28×2+28)
4. Диагональю призмы называется - отрезок, концами которого служат две вершины призмы, не лежащие на одной ее грани.
5. Прямоугольным параллелепипедом называется - прямая призма, основанием которой является прямоугольник.
6. Призма называется наклонной, если - ее боковые ребра не перпендикулярны основаниям.
7. Призма называется правильной, если - основанием которой является правильный многоугольник.
8. Площадью полной поверхности призмы называется сумма - всех боковых граней призмы.
9. Все двугранные углы при боковых гранях прямой призмы - прямые.
10. Площадь боковой поверхности куба с ребром 10 см равна - 600 см².
( так как у куба 4 боковых стороны и 2 основания, т.е. всего 6 квадратных сторон. А площадь одной стороны считается по формуле:
S = a², где а - длина стороны квадрата.
S = 10×10 = 100 см². - площадь одной стороны квадрата.
Тогда площадь всей поверхности куба:
S куба = 6×S
S куба = 6×100 = 600 см²).
11. Площадь полной поверхности куба с ребром 6 см равна - 216.
(так как грани куба - квадраты, площадь каждого квадрата равна
6² = 36. Куб состоит из шести таких квадратов значит площадь полной поверхности равна 36×6 = 216).
12. Площадь боковой поверхности правильной четырёхугольной призмы с высотой h и стороной основания a равна - Sб.п.= 4ah
13. Если диагональ куба равна d, то площадь полной поверхности куба равна - 2d²
(Так как S полy. пов. куба равна 6a² (а - ребро куба) ,
квадрат диагонали равен сумме квадратов всех измерений, тогда:
d²=3a² , тогда:
Sп.п. = 6a² = 2×(3a²) = 2d² )
14. Прямоугольный параллелепипед имеет три измерения, равные a=5 см, b=8 см, h =10 см. Площадь его полной поверхности равна - 340 см²
(Так как Sполн.пов. = Sбок. + 2Sосн.
Sбок. = Pосн. ×, S = 2×(5 + 8)×10 = 260 см²
Sосн. = а×в, S = 5×8 = 40 см²
Sполн. = 260 + 2×40 = 340 см²)
15.Площадь полной поверхности правильной треугольной призмы со стороной основания а и боковым ребром с равна - a²×√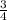
×c = a²×c×√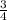
( Так как площадь основания равностороннего треугольника со стороной а = Sосн.= a²×√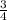
Таких оснований у призмы две.
Sбок.грани прямоугольника=
Sбок.гр. = a×c, таких граней три.
Sполн.пов. =
Sп.п. = 2×Sосн.+ 3×Sбок.гр. = a²×√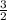
+ 3ac
Объем призмы =
V = Sосн.×H = a²×√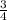
×c = a²×c×√
).
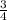Для того , чтобы найти сторону АD необходимо знать , что противоположные стороны у прямоугольника равны . следовательно AD=12, нам известно , что площадь прямоугольника равна 48 , для того , чтобы найти AB необходимо SABCD÷12=48÷12=4 т.к. противоположные стороны равны AB=CD=4
теперь найдем Pabcd=(12+4)*2=32
т.к. периметры у прямоугольника и у квадрата равны , то Pmklh=32
у квадрата все стороны равны их 4 для того , чтобы найти сторону квадрата нужно P÷4=32÷4=8 это и есть сторона квадрата