Рассмотрим 2 случая: для колоды из 36 карт и для колоды из 54 карт.
1. В колоде 36 карт. Тогда туз вытаскивается с вероятностью 4/36 (4 туза на 36 карт всего). 4/36 = 1/9. А вот король вытаскивается с вероятностью 4/35 (4 короля на 35 оставшихся после туза карт).
Итак: в этом случае для туза вероятность равна 1/9, для короля 4/35.
2. В колоде 54 карты. Тогда туз вытаскивается с вероятностью 4/54 (4 туза на 54 карты всего). А король вытаскивается с вероятностью 4/53 (4 короля на 53 оставшихся после туза карт).
Итак: в этом случае для туза вероятность равна 4/54, для короля 4/53.
Рассмотрим 2 случая: для колоды из 36 карт и для колоды из 54 карт.
1. В колоде 36 карт. Тогда туз вытаскивается с вероятностью 4/36 (4 туза на 36 карт всего). 4/36 = 1/9. А вот король вытаскивается с вероятностью 4/35 (4 короля на 35 оставшихся после туза карт).
Итак: в этом случае для туза вероятность равна 1/9, для короля 4/35.
2. В колоде 54 карты. Тогда туз вытаскивается с вероятностью 4/54 (4 туза на 54 карты всего). А король вытаскивается с вероятностью 4/53 (4 короля на 53 оставшихся после туза карт).
Итак: в этом случае для туза вероятность равна 4/54, для короля 4/53.
Пошаговое объяснение:
Проведём наклонную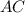
к плоскости 
.
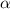Проведём из точки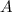
перпендикуляр 
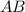к плоскости 
.
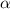Отрезок, соединяющий основание перпендикуляра с основанием наклонной, называется проекцией наклонной.Соединим точк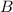и
и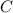 
и получим проекцию 
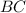наклонной 
.
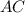Так как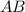
- перпендикуляр к плоскости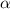 
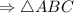- прямоугольный (где 
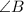- прямой)
Нам надо найти угол между наклонной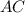
и плоскостью 
- 
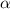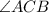
По определению косинуса острого угла в прямоугольном треугольнике,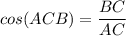
По таблице значений синуса, косинуса, тангенса острых углов получаем: