a) a+b+ 12
Сумма a, b и 12.
б) (2 +a)(b-с);
Произведение суммы 2 и а и разности b и с.
в)100 - (х+у);
Разность 100 и суммы x и y.
г) 4m - 8;
Разность произведения 4 и m и 8.
д) 6k + 3);
Предположу, что левая скобка стоит так: 6(k + 3)
Произведение 6 и суммы k и 3.
Если же правильная запись 6k + 3, то это сумма произведения 6 и k и 3.
е) а - с;
а+b
Предположу, что здесь имелась в виду эта дробь:
Частное разности a и c и суммы a и b&
ж) 2 + 4,5b;
Сумма 2 и произведения 4,5 и b&.
и) (n -7).
Разность n и 7.
b = 5
i = 3
Пошаговое объяснение:
Необходимо решить уравнение в простых числах:
b+i = (b-i)^3, откуда b-i > 0
Преобразуем уравнение:
(b-i) +2i = (b-i)^3
2i = (b-i)^3 - (b-i)
Рассмотрим общий случай: r ≠ 2; i≠2
А поскольку числа b и i - простые, то это значит, что они нечетные.
Откуда, число b - i является четным, то есть b-i = 2k, где k - натуральное число.
Таким образом:
2i = (2k)^3 - (2k)
2i = 2k( (2k)^2 - 1)
i = k(4k^2 - 1)
Число i является простым, а значит делится только на 1 и на само себя.
Учитывая, что при натуральном k: k <4k^2 - 1, то возможен только один вариант:
k = 1
4k^2 - 1 = i
Откуда:
i = 4*1^2 - 1 = 3 - простое число.
b-i = 2k = 2
b = i + 2 = 5 - простое число
То есть видим одно из решений:
i= 3
Рассмотрим теперь случай, когда одно из простых чисел b и i равно 2, но поскольку b>i, то i = 2
4 = (b-2)^3 -(b-2)
b-2 = t - натуральное нечетное число.
t^3 -t - 4 = 0
Откуда t - нечетный делитель числа 4, то есть t =1
1^3 - 1 - 4 ≠ 0
А значит этот вариант отпадает.
a) a+b+ 12
Сумма a, b и 12.
б) (2 +a)(b-с);
Произведение суммы 2 и а и разности b и с.
в)100 - (х+у);
Разность 100 и суммы x и y.
г) 4m - 8;
Разность произведения 4 и m и 8.
д) 6k + 3);
Предположу, что левая скобка стоит так: 6(k + 3)
Произведение 6 и суммы k и 3.
Если же правильная запись 6k + 3, то это сумма произведения 6 и k и 3.
е) а - с;
а+b
Предположу, что здесь имелась в виду эта дробь: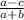
Частное разности a и c и суммы a и b&
ж) 2 + 4,5b;
Сумма 2 и произведения 4,5 и b&.
и) (n -7).
Разность n и 7.
b = 5
i = 3
Пошаговое объяснение:
Необходимо решить уравнение в простых числах:
b+i = (b-i)^3, откуда b-i > 0
Преобразуем уравнение:
(b-i) +2i = (b-i)^3
2i = (b-i)^3 - (b-i)
Рассмотрим общий случай: r ≠ 2; i≠2
А поскольку числа b и i - простые, то это значит, что они нечетные.
Откуда, число b - i является четным, то есть b-i = 2k, где k - натуральное число.
Таким образом:
2i = (2k)^3 - (2k)
2i = 2k( (2k)^2 - 1)
i = k(4k^2 - 1)
Число i является простым, а значит делится только на 1 и на само себя.
Учитывая, что при натуральном k: k <4k^2 - 1, то возможен только один вариант:
k = 1
4k^2 - 1 = i
Откуда:
i = 4*1^2 - 1 = 3 - простое число.
b-i = 2k = 2
b = i + 2 = 5 - простое число
То есть видим одно из решений:
i= 3
b = 5
Рассмотрим теперь случай, когда одно из простых чисел b и i равно 2, но поскольку b>i, то i = 2
2i = (b-i)^3 - (b-i)
4 = (b-2)^3 -(b-2)
b-2 = t - натуральное нечетное число.
t^3 -t - 4 = 0
Откуда t - нечетный делитель числа 4, то есть t =1
1^3 - 1 - 4 ≠ 0
А значит этот вариант отпадает.