Нам нужно выразить число в виде степени с основанием . Для этого стоит вспомнить что при возведении степени в степень, основание (или число) степени остаётся без изменения, а показатели степеней перемножаются. То есть наглядно это выглядит так:
То есть нам нужно разложить 20 степень так, чтобы . К счастью это не составит проблем, так как 20 без проблем делится на 5, чтобы найти второе число, после которого наше число можно записать как число со степенью в степени. Поэтому если 20 поделить на 5, то мы получим 4. То есть исходя из формулы выше , а значит все число имеет вид:
ответ: ( 0 ; 8 ) U ( 32 ; + ∞ ) .
Пошаговое объяснение:
log²₂ x - 8 log ₂ x + 15 >0 ; ОДЗ : х > 0 ;
заміна t = log ₂ x ; t² - 8t + 15 > 0 ; D = 4 > 0 ; t ₁= 3 ; t ₂ = 5 ; маємо :
t < 3 ; або t > 5 ;
log ₂ x < 3 log ₂ x > 5
log ₂ x < log ₂ 8 log ₂ x > log ₂ 2⁵ ;
{ x < 8 , { x > 32 ,
{ x > 0 ; { x > 0 ;
xЄ ( 0 ; 8 ) ; xЄ ( 32 ; + ∞ ) .
xЄ ( 0 ; 8 ) U ( 32 ; + ∞ ) .
Пошаговое объяснение:
Нам нужно выразить число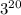 в виде степени с основанием
в виде степени с основанием 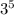 . Для этого стоит вспомнить что при возведении степени в степень, основание (или число) степени остаётся без изменения, а показатели степеней перемножаются. То есть наглядно это выглядит так:
. Для этого стоит вспомнить что при возведении степени в степень, основание (или число) степени остаётся без изменения, а показатели степеней перемножаются. То есть наглядно это выглядит так: 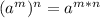
То есть нам нужно разложить 20 степень так, чтобы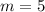 . К счастью это не составит проблем, так как 20 без проблем делится на 5, чтобы найти второе число, после которого наше число можно записать как число со степенью в степени. Поэтому если 20 поделить на 5, то мы получим 4. То есть исходя из формулы выше
. К счастью это не составит проблем, так как 20 без проблем делится на 5, чтобы найти второе число, после которого наше число можно записать как число со степенью в степени. Поэтому если 20 поделить на 5, то мы получим 4. То есть исходя из формулы выше 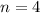 , а значит все число имеет вид:
, а значит все число имеет вид: