Для начала рассмотри первое неравенство системы, оно похоже на функцию окружности. Преобразуем это неравенство и посмотрим:
в выражении выделим полный квадрат:
Действительно, получили функцию окружности с радиусом 4 и перемещенную вдоль оси абсцисс на единиц. Знак неравенства означает что решение лежит "внутри" окружности.
Теперь рассмотрим второе неравенство системы, попробуем его преобразовать:
сделаем замену: , тогда можем записать так: отсюда получаем делаем обратную замену: в данной системе неравенств выражаем переменную y:
Из этой системы неравенств можем записать двойное неравенство:
; отсюда делаем вывод что графиком неравенства является две прямые, а именно в первом случае будет график прямой с штриховкой выше данной прямой.
Во втором случаем будет график прямой с штриховкой ниже данной прямой. Из всего выше сказанного про второе неравенство системы делаем вывод что графиком данного неравенства будут две прямые с штриховкой между этими прямыми. Изобразим данный график(изображение графика на рисунке ниже).
Теперь разберемся с первым неравенством системы: Поскольку это окружность радиуса 4, то ее площадь будет равна . Данная окружность лежит внутри прямых, где при различных значениях b мы ее можем передвигать вдоль оси абсцисс, тем самым меняя ее площадь. Необходимо указать те значения параметра b при которых площадь будет равна , т.е половина окружности. Отсюда становится понятно что ее площадь будет равна (т.е половине) в той точке, где прямая отсечет от нее половину.
В случае с прямой , то значение параметра , тогда окружность становится на точку -5 по оси абсцисс, где прямая пересекает данную окружность в двух точках, и проходит через центр (точка -5), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых , значит решение(на рисунке ниже показана окружность при b=-5 и прямые которые отсекают нужную площадь)
В случае с прямой В случае с прямой , то значение параметра , тогда окружность становится на точку 7 по оси абсцисс, где прямая пересекает данную окружность в двух точках, и проходит через центр (точка 7), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых , значит решение(на рисунке ниже показана окружность при b=7 и прямые которые отсекают нужную площадь)
Обозначим эти числа а и b. НОД(a,b) обозначим n.
Тогда можно написать:
a = n*m; b = n*k.
Произведение чисел на 15 больше n.
ab = n + 15
n*m*n*k = n + 15
(mk)*n^2 - n - 15 = 0
можно решить как квадратное уравнение.
D = (-1)^2 - 4*(-15)*mk = 60mk + 1
Чтобы n было натуральным числом, D должно быть точным квадратом.
D = 60mk + 1 = p^2 > 1; p > 1
n1 = (1 - p)/(2mk) < 0, так как m>0, k>0, p>1 - не подходит
n2 = (1+p)/(2mk) > 0 - подходит.
Теперь найдем максимум этой функции относительно mk, учитывая, что p = √(60mk+1)
n = (1 + √(60mk+1)) / (2mk)
Например, при mk = 2 получаем:
D = 60*2 + 1 = 121 = 11^2
n = (1 + √121)/(2*2) = (1+11)/4 = 12/4 = 3
При mk = 6 получаем:
D = 60*6 + 1 = 361 = 19^2
n = (1 + 19) / (2*6) = 20/6 - нецелое.
Наверное, это mk = 2, то есть наибольшее - 2
Пошаговое объяснение:
Для начала рассмотри первое неравенство системы, оно похоже на функцию окружности. Преобразуем это неравенство и посмотрим:
Теперь рассмотрим второе неравенство системы, попробуем его преобразовать:
Из этой системы неравенств можем записать двойное неравенство:
Во втором случаем будет график прямой с штриховкой ниже данной прямой. Из всего выше сказанного про второе неравенство системы делаем вывод что графиком данного неравенства будут две прямые
будет график прямой с штриховкой ниже данной прямой. Из всего выше сказанного про второе неравенство системы делаем вывод что графиком данного неравенства будут две прямые 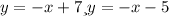 с штриховкой между этими прямыми. Изобразим данный график(изображение графика на рисунке ниже).
с штриховкой между этими прямыми. Изобразим данный график(изображение графика на рисунке ниже).
Теперь разберемся с первым неравенством системы: Поскольку это окружность радиуса 4, то ее площадь будет равна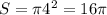 . Данная окружность лежит внутри прямых, где при различных значениях b мы ее можем передвигать вдоль оси абсцисс, тем самым меняя ее площадь. Необходимо указать те значения параметра b при которых площадь будет равна
. Данная окружность лежит внутри прямых, где при различных значениях b мы ее можем передвигать вдоль оси абсцисс, тем самым меняя ее площадь. Необходимо указать те значения параметра b при которых площадь будет равна 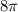 , т.е половина окружности. Отсюда становится понятно что ее площадь будет равна
, т.е половина окружности. Отсюда становится понятно что ее площадь будет равна 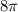 (т.е половине) в той точке, где прямая отсечет от нее половину.
(т.е половине) в той точке, где прямая отсечет от нее половину.
В случае с прямой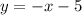 , то значение параметра
, то значение параметра 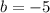 , тогда окружность становится на точку -5 по оси абсцисс, где прямая
, тогда окружность становится на точку -5 по оси абсцисс, где прямая 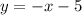 пересекает данную окружность в двух точках, и проходит через центр (точка -5), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых
пересекает данную окружность в двух точках, и проходит через центр (точка -5), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых 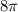 , значит
, значит 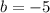 решение(на рисунке ниже показана окружность при b=-5 и прямые которые отсекают нужную площадь)
решение(на рисунке ниже показана окружность при b=-5 и прямые которые отсекают нужную площадь)
В случае с прямой В случае с прямой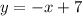 , то значение параметра
, то значение параметра 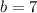 , тогда окружность становится на точку 7 по оси абсцисс, где прямая
, тогда окружность становится на точку 7 по оси абсцисс, где прямая 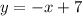 пересекает данную окружность в двух точках, и проходит через центр (точка 7), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых
пересекает данную окружность в двух точках, и проходит через центр (точка 7), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых 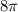 , значит
, значит 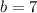 решение(на рисунке ниже показана окружность при b=7 и прямые которые отсекают нужную площадь)
решение(на рисунке ниже показана окружность при b=7 и прямые которые отсекают нужную площадь)
Получаем