5/8 которого равны 2 1/2; 2/5 которого равны 3 3/4
2/3 которого равны 5 1/3
3/4 которого равны 3/14.

Показать ответ

Ответ:

простоя43

03.05.2020 01:55

В песочнице лежат только 3 вида игрушек: деревянные кубики, пластиковые кубики и пластиковые пирамидки. Известно, что пирамидок в 4 раза меньше, чем кубиков, а пластиковых игрушек в 9 раз больше, чем деревянных. Какую часть от всех игрушек, лежащих в песочнице, составляют пластиковые кубики?
Дер. куб.   }
Пл.куб   } в 4р. больше }
Пл.пир    } в 9 раз больше

1+9=10 - частей составляют пластиковые и деревян. игрушки
1+4=5 - частей составл. кубики и пирамидки
10:5=2 - части от всех пластиковых игрушек составляют пирамидки
9-2=7 - частей от пластиковых игрушек составляют пласт.кубики
7:10=7/10 - от всех игрушек составляют пластиковые кубики
Проверка:
Дер. куб. 1
Пл.куб 7
Пл.пир      2 .
(1+7):2=4
(2+7):1=9

2)На полке стоят только 3 вида книг: грустные сказки, весёлые сказки и весёлые рассказы. Известно, что рассказов в 3 раза меньше, чем сказок, а количество грустных книг в 7 раз меньше, чем веселых. Какую часть от всех книг, стоящих на полке, составляют веселые сказки?
7+1=8 - частей веселых и грустных книг
3+1=4 - части сказок и рассказов
8:4=2 - части веселых и грустных книг составляют веселые рассказы
7-2=5 - частей от веселых книг составляют веселые сказки
5:8=5/8 - всех книг составляют веселые сказки
Проверка:
гр. ск - 1
вес. ск - 5
вес. расск. - 2
(1+5):2=3
(5+2):1=7

0,0(0 оценок)

Ответ:

glushcovapolia

03.05.2020 01:55

$(x + 1)|x-2| = a^{2}$

Первый аналитический)

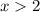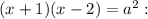
1) Если x 2 , то $(x + 1)(x-2) = a^{2}:$

$x^{2}-x-2 = a^{2}$

$x^{2} - x - 2 - a^{2} = 0$

$x^{2} - x - (2 + a^{2}) = 0$

$D = (-1)^{2} + 4(2 + a^{2}) = 1+8 + 4a^{2} = 9 + 4a^{2} 0$

$x_{1,2} = \dfrac{1 \pm \sqrt{9 + 4a^{2}}}{2}$

Проверим условие x 2:

$1.1) \ \dfrac{1 + \sqrt{9 + 4a^{2}}}{2} 2$

$1 + \sqrt{9 + 4a^{2}} 4$

$\sqrt{9 + 4a^{2}} 3$

$9 + 4a^{2} 9$

$4a^{2} 0$

$a \neq 0$

$1.2) \ \dfrac{1 - \sqrt{9 + 4a^{2}}}{2} 2$

$1 - \sqrt{9 + 4a^{2}} 4$

$\sqrt{9 + 4a^{2}} < -3$

$a \in \varnothing$

Таким образом, если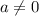 $a \neq 0$ , то имеем корень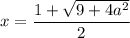 $x = \dfrac{1 + \sqrt{9 + 4a^{2}}}{2}$

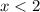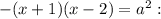
2) Если x < 2 , то $-(x + 1)(x-2) = a^{2}:$

$x^{2}-x-2 = -a^{2}$

$x^{2} - x - 2 + a^{2} = 0$

$x^{2} - x - (2 - a^{2}) = 0$

$D = (-1)^{2} + 4(2 - a^{2}) = 1+8 - 4a^{2} = 9 - 4a^{2}$

Найдем такие значения , при которых D 0:

$9 - 4a^{2} 0$

$4a^{2} < 9$

$\sqrt{4a^{2}} < \sqrt{9}$

2|a| < 3

$a \in \left(-\dfrac{3}{2}; \ \dfrac{3}{2} \right)$

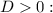
Тогда корни:

$x_{1,2} = \dfrac{1 \pm \sqrt{4 - 9a^{2}}}{2}$

Проверим условие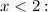 x < 2:

$2.1) \ \dfrac{1 + \sqrt{9 - 4a^{2}}}{2} < 2$

$1 + \sqrt{9 - 4a^{2}} < 4$

$\sqrt{9 - 4a^{2}} < 3$

$9 - 4a^{2} < 9$

$-4a^{2} < 0$

$4a^{2} 0$

$a \neq 0$

$2.2) \ \dfrac{1 - \sqrt{9 - 4a^{2}}}{2} < 2$

$1 - \sqrt{9 - 4a^{2}} < 4$

$\sqrt{9 - 4a^{2}}-3$

$a \in \left[-\dfrac{3}{2}; \ \dfrac{3}{2} \right]$

С учетом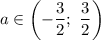 $a \in \left(-\dfrac{3}{2}; \ \dfrac{3}{2} \right)$ имеем: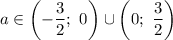 $a \in \left(-\dfrac{3}{2}; \ 0 \right) \cup \left(0; \ \dfrac{3}{2} \right)$

Таким образом, при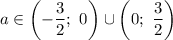 $a \in \left(-\dfrac{3}{2}; \ 0 \right) \cup \left(0; \ \dfrac{3}{2} \right)$ имеем три корня.

Второй графический)

Рассмотрим две функции:

f(x) = (x+1)|x-2|

$g(x) = a^{2}$ — линейная функция, график — прямая, параллельная оси абсцисс

Изобразим на координатной плоскости функцию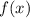 f(x)

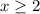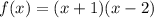1) Если $x \geq 2$ , то f(x) = (x + 1)(x-2) — квадратичная функция, график — парабола, ветви параболы направлены вверх

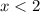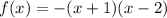2) Если x < 2 , то f(x) = -(x + 1)(x-2) — квадратичная функция, график — парабола, ветви параболы направлены вниз

Вершина параболы: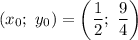 $(x_{0}; \ y_{0}) = \left(\dfrac{1}{2}; \ \dfrac{9}{4} \right)$

Изобразим данные функции на соответствующих участках (см. вложение).

Уравнение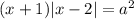 $(x + 1)|x-2| = a^{2}$ будет иметь три корня, если будет три пересечения графика функции f(x) = (x+1)|x-2| c $g(x) = a^{2}$

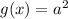
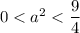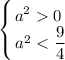
Так будет, если $0< a^{2} < \dfrac{9}{4}$ или $\displaystyle \left \{ {{a^{2} 0 \ } \atop {a^{2} < \dfrac{9}{4} }} \right.$

$\displaystyle \left \{ {{a \neq 0 \ \ \ \ \ \ \ \ \ \ \ \, } \atop {a \in \left(-\dfrac{3}{2}; \ \dfrac{3}{2} \right)}} \right.$

Решением системы будет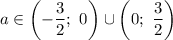 $a \in \left(-\dfrac{3}{2}; \ 0 \right) \cup \left(0; \ \dfrac{3}{2} \right)$

Таким образом, при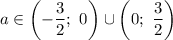 $a \in \left(-\dfrac{3}{2}; \ 0 \right) \cup \left(0; \ \dfrac{3}{2} \right)$ имеем три корня.

ответ: $a \in \left(-\dfrac{3}{2}; \ 0 \right) \cup \left(0; \ \dfrac{3}{2} \right)$

Найдите значения параметра а, при которых уравнение (x+1)|x-2|=a^2 имеет три корня.

0,0(0 оценок)

Популярные вопросы: Математика

мари13121

19.11.2022 20:04

Два пешехода одновременно вышли из одного пункта и движутся в противоположных направлениях скорость одного 100 метров в минуту а другой 80 метров в минуту какое расстояние...

serbinaluba66cet

19.11.2022 20:04

Самое распространенное растение заливных луг...

Юролика

19.11.2022 20:04

779. длина прямоугольного участка земли 43 м, а его ширина на 15 м меньше длины. найдите периметр и площадь участка. 780. длина прямоугольного поля 300 м, а ширина 200 м. найдите...

anghelina1

19.11.2022 20:04

20 б найдите значения выражений а)24а+47а+53а+76а= ,если а=47 б)128р-72р-28р,если р=11...

Dezzy12

19.11.2022 20:04

Сколько будет,если от одного градуса вычесть одну минуту сколько будет если от одного градуса вычесть 59 минут 55 секунд...

OsamuDazai

19.11.2022 20:04

Мари 12 лет но у неё был день день рождения всего 3 раза почему?...

Ника6258227

19.11.2022 20:04

Вычисли с числового луча 12: 4,10: 5,14: 7,18: 6...

bauka077

19.11.2022 20:04

Сколько существует натуральных четных двузначных чисел которые делятся на число 13 без остатка...

damiramirov321

19.11.2022 20:04

Бабушка посадила 36 луковиц тюльпанов. внучка посадила в 4 раза меньше чем бабушка. а внук-в 9 раз меньше чем бабушка и внучка вместе. сколько луковиц тюльпанов посадил внук....

ybrybrybrybrrby

24.03.2020 00:05

Решите : разность двух чисел 342.одно их них в 7 раз меньше другого.найдите эти числа....

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку

5/8 которого равны 2 1/2; 2/5 которого равны 3 3/42/3 которого равны 5 1/33/4 которого равны 3/14.​

5/8 которого равны 2 1/2; 2/5 которого равны 3 3/4
2/3 которого равны 5 1/3
3/4 которого равны 3/14.