5. Есептерді шығар. а) Спортзалда таңғы жаттығуға 14 ұл, олардан 7-еуі артық қыз
сапқа тұрғызылды. Барлығы неше бала сапқа тұрғызылды?
ә) Спортзалда 12 футбол добы, одан 4-еуі кем волейбол добы бар.
Ал футбол мен волейбол добы бірге қанша болса, сонша теннис
добы бар. Залда неше теннис добы бар?

Показать ответ

Ответ:

medi8

08.10.2022 20:09

$C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

или

$2\,\,753\,\,294\,\,408\,\,504\,\,640$

Пошаговое объяснение:

Давайте сначала введём понятие.

Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать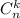 C^k_n и определим формулой

$\displaystyle C^k_n=\frac{n!}{k!(n-k)!}$

Если нужно доказательство, пишите

Итак, приступаем к решению.

Сначала раздаем первому игроку.

Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.

$\displaystyle C^{10}_{32}=\frac{32!}{10!(32-10)!}= \frac{22!*23*24*25*26*27*...*32}{22!*10*9*8*7*6*5*4*3*2} =\\=\frac{23*24*25*26*37*...*35}{10*9*8*7*6*5*4*3*2}=64512240$

Но можно было просто оставить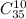 $C^{10}_{35}$

Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.

Тогда количество раздать второму 10 карт из 22 - это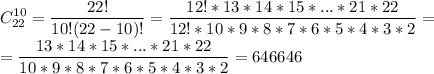 $\displaystyle C^{10}_{22}=\frac{22!}{10!(22-10)!}=\frac{12!*13*14*15*...*21*22}{12!*10*9*8*7*6*5*4*3*2}=\\=\frac{13*14*15*...*21*22}{10*9*8*7*6*5*4*3*2}=646646$

Или опять же можно было бы оставить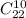 $C^{10}_{22}$

Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно

$\displaystyle C^{10}_{12}=\frac{12!}{10!(12-10)!}=\frac{12*11*10!}{10!*2}=66$

Ну хоть здесь нормальное число. Но опять же можно было и оставить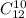 $C^{10}_{12}$

И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.

Получим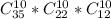 $C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

Или если в числах, то это

$64512240*646646*66=2753294408504640=2\,\,753\,\,294\,\,408\,\,504\,\,640$

0,0(0 оценок)

Ответ:

Diglir

09.03.2023 09:59

х л - объем сосуда, отсюда

х л – первоначальное количество глицерина

Первое переливание.

(х - 1) - количество глицерина после первого переливания

(х-1)/х - количество глицерина в частях от всего объема сосуда, т.е. концентрация смеси после первого переливания.

Второе переливание.

Найдём количество глицерина в частях от концентрации первой смеси, это и будет концентрация смеси после второго переливания.

(х - 1)/х от (х – 1)/х = (х – 1)²/х² = ((х-1)/х)² - количество глицерина в частях от всего объема сосуда, т.е. концентрация смеси после второго переливания

Третье переливание.

Найдём количество глицерина в частях от концентрации второй смеси, это и будет концентрация смеси после третьего переливания.

(х - 1)/х от ((х – 1)/х)² = (х – 1)³/х³ = ((х-1)/х)³ - концентрация смеси после третьего переливания

По условию после третьего переливания

глицерин составляет 1 часть, а вода – 7 частей

1 + 7 = 8 частей – составляет вся смесь, которая занимает весь объём

Отсюда 1/8 - концентрация смеси после третьего переливания

Имеем уравнение

((х-1)/х)³ = 1/8

((х-1)/х)³ = (1/2)³

х-1/х = ½

2 * (х-1) = х * 1