5. Учащихся попросили назвать их любимый вкус мороженого. диаграмме представлена информация об их ответах. Известно, что сливочное мороженое предпочитают 12 учащихся Используя данные на диаграмме, ответьте на вопросы. да не а) Сколько учащихся предпочитают фисташковое мороженое? b) Какой угол на диаграмме соответствует наименованию «Клубничное мороженое»? C) Сколько учащихся любят клубничное мороженое?
OM=60 – расстояние от центра O окружности до хорды AB
ON=52 – расстояние от центра O окружности до хорды CD
Найти: x=CD – длину второй хорды
Решение.
Так как OA=OB=OC=OD и равны радиусу R окружности, то получаем равнобедренные треугольники OAB и OCD. По условию, расстояние от центра O окружности до хорды AB, то есть длина отрезка OM, перпендикулярного к отрезке AB, равно 60. Точно также, расстояние от центра O окружности до хорды CD, то есть длина отрезка ON, перпендикулярного к отрезке CD, равно 52.
Но, по свойству равнобедренных треугольников, перпендикуляры OM и ON к основанию равнобедренных треугольников, соответственно, OAB и OCD является высотой, медианой и биссектрисой. Тогда медианы OM и ON делят, соответственно, основание равнобедренных треугольников OAB и OCD пополам. Отсюда получаем:
1) длина MB=50:2=25 и длина ND=x:2;
2) треугольники OMB и OND прямоугольные с гипотенузой, равной радиусу R.
Применим теорему Пифагора к прямоугольному треугольнику OMB и находим R:
78 (единиц)
Пошаговое объяснение:
Дано (см. рисунок):
Окружность радиуса R
AB=50 – длина первой хорды
OM=60 – расстояние от центра O окружности до хорды AB
ON=52 – расстояние от центра O окружности до хорды CD
Найти: x=CD – длину второй хорды
Решение.
Так как OA=OB=OC=OD и равны радиусу R окружности, то получаем равнобедренные треугольники OAB и OCD. По условию, расстояние от центра O окружности до хорды AB, то есть длина отрезка OM, перпендикулярного к отрезке AB, равно 60. Точно также, расстояние от центра O окружности до хорды CD, то есть длина отрезка ON, перпендикулярного к отрезке CD, равно 52.
Но, по свойству равнобедренных треугольников, перпендикуляры OM и ON к основанию равнобедренных треугольников, соответственно, OAB и OCD является высотой, медианой и биссектрисой. Тогда медианы OM и ON делят, соответственно, основание равнобедренных треугольников OAB и OCD пополам. Отсюда получаем:
1) длина MB=50:2=25 и длина ND=x:2;
2) треугольники OMB и OND прямоугольные с гипотенузой, равной радиусу R.
Применим теорему Пифагора к прямоугольному треугольнику OMB и находим R:
R² = OM²+MB² = 60²+25² = 3600+625 = 4225 = 65² или R=65.
Применим теорему Пифагора к прямоугольному треугольнику OCD:
R² = ON²+ND² = 52²+(x:2)² или
(x:2)² = R²–52² = 65²–52² = 4225–2704 = 1521 = 39² или
x:2 = 39.
Отсюда CD=x=39·2 = 78 (единиц).
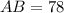ед.
Пошаговое объяснение:Обозначим окружность с центром в точке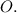
===========================================================
Если радиус окружности перпендикулярен к хорде окружности, то он делит хорду пополам.Рассмотрим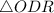
:
Найдём радиус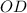
по теореме Пифагора:
===========================================================
Так как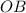
и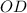 
- радиусы окружности 
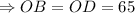ед.
Рассмотрим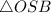
:
Найдём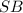
по теореме Пифагора:
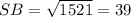ед.
Если радиус окружности перпендикулярен к хорде окружности, то он делит хорду пополам.