Найдем сначала наименьшее значение то есть наименьшее расстояние от точек прямой 2x+3y=5 до начала координат; иными словами - длину перпендикуляра, опущенного из начала координат на эту прямую. Прямая пересекает оси координат в точках A(5/2;0) и B(0;5/3). Обозначим O(0;0); длина перпендикуляра будет совпадать с высотой треугольника ABO, опущенной из вершины прямого угла, а она может быть посчитана как произведение катетов, деленное на гипотенузу (эта формула следует из того, что площадь прямоугольного треугольника равна половине произведения катетов, а также половине произведения гипотенузы на эту высоту). Катеты равны 5/2 и 5/3, а гипотенуза находится по теореме Пифагора и равна Поэтому высота равна А наименьшее значение суммы квадратов икса и игрека будет равно
Конечно, ответ можно было получить проще, но приведенный , на мой взгляд, самый наглядный.
Найдем сначала наименьшее значение
то есть наименьшее расстояние от точек прямой 2x+3y=5 до начала координат; иными словами - длину перпендикуляра, опущенного из начала координат на эту прямую. Прямая пересекает оси координат в точках A(5/2;0) и B(0;5/3). Обозначим O(0;0); длина перпендикуляра будет совпадать с высотой треугольника ABO, опущенной из вершины прямого угла, а она может быть посчитана как произведение катетов, деленное на гипотенузу (эта формула следует из того, что площадь прямоугольного треугольника равна половине произведения катетов, а также половине произведения гипотенузы на эту высоту). Катеты равны 5/2 и 5/3, а гипотенуза находится по теореме Пифагора и равна 
Поэтому высота равна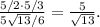 
А наименьшее значение суммы квадратов икса и игрека будет равно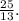 
Конечно, ответ можно было получить проще, но приведенный , на мой взгляд, самый наглядный.
ответ: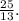
Пошаговое объяснение:
Чтобы найти площадь окружности, нужно знать её радиус или диаметр.
Формула для нахождения площади окружности :
S = πR² или S = π(D:2)²
Где π - математическая константа, выражающая отношение длины окружности к длине её диаметра и равно 3,14
R - радиус
D - диаметр
К примеру, если известно что радиус окружности = 5 см, нужно найти площадь:
S = πR²
S = 3,14 * 5² = 3,14 * 25 = 78,5 см²
Если нам известен диаметр окружности и к примеру и он равен 12 см :
S = π(D : 2)²
S = π(12 : 2)² = 3,14 * 6² = 3,14 * 36 = 113,04 см²