На танец не было приглашено 1/4 дам. Значит было приглашено 3/4 дам. На танец никого не пригласили 2/7 джентльменов, значит пригласили на танец 5/7 джентльменов. Пусть количество равно x, а количество джентльменов y. Количество дам приглашенных на танец, равно количеству джентльменов которые пригласили на танец.
Значит 3/4x=5/7y. Дамножим обе части уравнения на 28. Тогда получится. 21x=20y. Поскольку у чисел 20 и 21, нет общих множетелей, единственное возможное решение данного уравнения, это x=20, y=21. Значит было 20 дам и 21 джентльмен. Значит всего на балу было 20+21=41 человек.
Число двузначное. Пусть его цифры a - цифра десятков и b - цифра единиц. По условию, .
Поскольку a и b целые и не меньше нуля, то можно попробовать подобрать.
1) не подходят, т.к. число (вставили между а и b цифру 1, получили a1b) в действительности двузначное, и
2) также не подходят, т.к. (здесь не произведения чисел, а десятичная запись)
3) . Проверяем: (верно, т.е. совпадает с условием). Тогда задуманное двузначное число равно 21, и, вставляя число 1 между 2 и 1, получаем число 211.
На этом, казалось бы все, но осталась еще одна возможная комбинация: . Вообще говоря, пока ничего не мешает и для нее выполняться условиям задачи. Что ж, проверяем: . Ан нет, для этой комбинации выполняются не все условия задачи.
Поскольку мы перебрали все возможные комбинации, то нам ничего не остается, как сказать, что задача имеет ровно одно решение: .
Классический метод
Этот метод стандартный, но он общий, и очень удобный (просто нам повезло с данными)
Число двузначное. Пусть его цифры a - цифра десятков и b - цифра единиц. Тогда искомое число равно (ВНИМАНИЕ! Здесь 10a уже обозначает умножение числа 10 на число a, здесь и далее будем подразумевать именно это). По условию, . По другому условию задачи, если мы вставим 1 между цифрами a и b, то получим число . По условию, вычитая из этого числа искомое двузначное получаем:
. Отсюда можно выразить a:
Подставляя a в уравнение , находим, что
Получаем, что искомое двузначное число равно 21.
Эпилог
Двумя методами получили одинаковый результат, следовательно, с большой вероятностью все сделано верно.
41
Пошаговое объяснение:
На танец не было приглашено 1/4 дам. Значит было приглашено 3/4 дам. На танец никого не пригласили 2/7 джентльменов, значит пригласили на танец 5/7 джентльменов. Пусть количество равно x, а количество джентльменов y. Количество дам приглашенных на танец, равно количеству джентльменов которые пригласили на танец.
Значит 3/4x=5/7y. Дамножим обе части уравнения на 28. Тогда получится. 21x=20y. Поскольку у чисел 20 и 21, нет общих множетелей, единственное возможное решение данного уравнения, это x=20, y=21. Значит было 20 дам и 21 джентльмен. Значит всего на балу было 20+21=41 человек.
Оригинальный метод:
Число двузначное. Пусть его цифры a - цифра десятков и b - цифра единиц. По условию,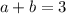
.
Поскольку a и b целые и не меньше нуля, то можно попробовать подобрать.
1)
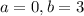не подходят, т.к. число 
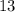(вставили между а и b цифру 1, получили a1b) в действительности двузначное, и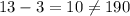 
2)
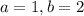также не подходят, т.к. 
(здесь 
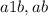не произведения чисел, а десятичная запись)
3)
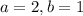. Проверяем: 
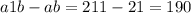(верно, т.е. совпадает с условием). Тогда задуманное двузначное число равно 21, и, вставляя число 1 между 2 и 1, получаем число 211.
На этом, казалось бы все, но осталась еще одна возможная комбинация: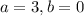
. Вообще говоря, пока ничего не мешает и для нее выполняться условиям задачи. Что ж, проверяем: 
. Ан нет, для этой комбинации выполняются не все условия задачи.
Поскольку мы перебрали все возможные комбинации, то нам ничего не остается, как сказать, что задача имеет ровно одно решение: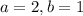
.
Классический метод
Этот метод стандартный, но он общий, и очень удобный (просто нам повезло с данными)
Число двузначное. Пусть его цифры a - цифра десятков и b - цифра единиц. Тогда искомое число равно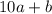
(ВНИМАНИЕ! Здесь 10a уже обозначает умножение числа 10 на число a, здесь и далее будем подразумевать именно это). По условию, 
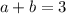. По другому условию задачи, если мы вставим 1 между цифрами a и b, то получим число 
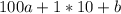. По условию, вычитая из этого числа искомое двузначное получаем:
Подставляя a в уравнение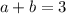
, находим, что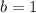 
Получаем, что искомое двузначное число равно 21.
Эпилог
Двумя методами получили одинаковый результат, следовательно, с большой вероятностью все сделано верно.