637. 1) Из 36 учеников 6 класса девять учащихся получили за контроль работу по математике оценку «5». Сколько процентов учася по чиши оценку «5»? 2) найдите процент содержания соли
1)При варке мясо теряет 35% своего веса.Сколько нужно взять сырного мяса, чтобы получить 520 грамм варённого?
Решение: потеря 35% означает, что 100-35=75% остается в результате
тогда:
520 гр = 75%
х гр = 100%
520 гр * 100% /75% = 639.33 гр мяса требуется изначально
ответ 639.33 грамма
4)Когда у пастуха спросили сколько у него лошадей, он ответил что 60 лошадей пьют воду, а остальные 0,6 всех лошадей пасутся.Сколько лошадей в табуне?
60 лошадей это 1-0.6=0.4 от всего количества
тогда
60л = 0.4
Хл = 1
60*1/0.4 = 150 лошадей всего
ответ 150 Лошадей
5) В классе 30 учащихся из них 17 занимаются в секции лыжников, а 11 в секции плавания и 3 в обеех секциях.Сколько учащихся этого класса не занимаются ни в одной из этих секций?
3 из 17 занимаются плаванием
значит только лыжами занимается 17-3=14 учеников
3 из 11 занимаются лыжами
значит только плаванием занимается 11-3=8 учеников
всего в секциях занимаются 14 лыжников + 8 плавцов +3 плавающих лыжника )))
итого в секциях занимаются 14+8+3=25 учеников
тогда 30-25=5 учеников которые не занимаются в секциях
На самом деле такое число найдётся для любой натуральной степени .
Я утверждаю, что для всех k найдётся число, состоящее из k цифр, не содержащее нулей в десятичной записи и делящееся на .
Доказываем по индукции.
База индукции. Для k = 1 подходит .
Индукционный переход. Пусть длина числа равна k, десятичная запись этого числа не содержит нулей. Припишем к этому числу слева ненулевую цифру a и потребуем, чтобы получившееся число делилось на .
Получившееся число равно , оно будет делиться на , если делится на 5.
при делении на 5 может давать остатки 1, 2, 3 и 4; n может давать любые остатки от 0 до 4. Ниже в таблице я явно выписываю, какие можно взять a для каждой комбинации остатков. Например, если n даёт остаток 3 при делении на 5; даёт остаток 4 при делении на 2, то можно взять a = 3: тогда даёт такой же остаток при делении на 5, что и .
Таким образом, если для k такое число найдётся, то и для k + 1, а значит, и для всех k, в том числе и для k = 1987.
Вот, например, числа, построенные для k от 1 до 20:
1)При варке мясо теряет 35% своего веса.Сколько нужно взять сырного мяса, чтобы получить 520 грамм варённого?
Решение: потеря 35% означает, что 100-35=75% остается в результате
тогда:
520 гр = 75%
х гр = 100%
520 гр * 100% /75% = 639.33 гр мяса требуется изначально
ответ 639.33 грамма
4)Когда у пастуха спросили сколько у него лошадей, он ответил что 60 лошадей пьют воду, а остальные 0,6 всех лошадей пасутся.Сколько лошадей в табуне?
60 лошадей это 1-0.6=0.4 от всего количества
тогда
60л = 0.4
Хл = 1
60*1/0.4 = 150 лошадей всего
ответ 150 Лошадей
5) В классе 30 учащихся из них 17 занимаются в секции лыжников, а 11 в секции плавания и 3 в обеех секциях.Сколько учащихся этого класса не занимаются ни в одной из этих секций?
3 из 17 занимаются плаванием
значит только лыжами занимается 17-3=14 учеников
3 из 11 занимаются лыжами
значит только плаванием занимается 11-3=8 учеников
всего в секциях занимаются 14 лыжников + 8 плавцов +3 плавающих лыжника )))
итого в секциях занимаются 14+8+3=25 учеников
тогда 30-25=5 учеников которые не занимаются в секциях
ответ: 5
Существует
Пошаговое объяснение:
На самом деле такое число найдётся для любой натуральной степени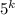 .
.
Я утверждаю, что для всех k найдётся число, состоящее из k цифр, не содержащее нулей в десятичной записи и делящееся на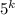 .
.
Доказываем по индукции.
База индукции. Для k = 1 подходит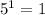 .
.
Индукционный переход. Пусть длина числа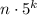 равна k, десятичная запись этого числа не содержит нулей. Припишем к этому числу слева ненулевую цифру a и потребуем, чтобы получившееся число делилось на
равна k, десятичная запись этого числа не содержит нулей. Припишем к этому числу слева ненулевую цифру a и потребуем, чтобы получившееся число делилось на 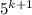 .
.
Получившееся число равно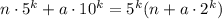 , оно будет делиться на
, оно будет делиться на 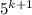 , если делится на 5.
, если делится на 5.
Таким образом, если для k такое число найдётся, то и для k + 1, а значит, и для всех k, в том числе и для k = 1987.
Вот, например, числа, построенные для k от 1 до 20:
5 25 125 3125 53125 453125 4453125 14453125 314453125 2314453125 22314453125 122314453125 4122314453125 44122314453125 444122314453125 4444122314453125 54444122314453125 254444122314453125 1254444122314453125 21254444122314453125Например, число 21254444122314453125 делится на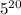 и не содержит нулей :)
и не содержит нулей :)