653. Представьте в виде бесконечной десятичной дроби число: 7
1
1)
2) ; 3) 28; -4
3
5
5) 7
19

Показать ответ

Ответ:

mazyrovavlada

29.05.2020 20:36

1 Сумма двух чисел больше одного из них на 12 и больше другого на 18.Найди эту сумму.

1слогаемое+2слогаемое=сумма

Сумма двух чисел больше одного из них на 12, т.е. одно из слогаемых 12.

Сумма двух чисел больше другого на 18, т.е. другое слогаемое 18

Т.о. получаем, что 18+12=30

2 Вычетаемое меньше уменьшаемого на 32. Найди разность.

чтобы узнать на сколько одно число меньше другого, надо из большего вычесть меньшее.

Бошее - это уменьшаемое, меньшее вычитаемое. Т.о. получается что их разница, это разность. Нам сказано, что вычитаемое меньше уменьшаемго на 32, значит разность =32.

0,0(0 оценок)

Ответ:

lidiyamartin9

21.03.2023 21:39

ответ: (e-1)/3

Пошаговое объяснение:

Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.

$\int{e^{x^{3} }x^2 } \, dx$ .

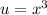Пусть u=x^3 , тогда $x=\sqrt[3]{u}$ .

$du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}$

Делаем подстановку в наше изначальное выражение:

$\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }$

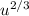Здесь $u^{2/3}$ сокращаются и мы имеем 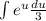$\int{e^u\frac{du}{3}}$ . Выносим 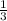$\frac{1}{3}$ за интеграл: 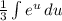$\frac{1}{3} \int{e^u} \, du$ . Теперь мы имеем знакомый интеграл, который равняется 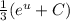$\frac{1}{3} (e^{u}+C)$ , тоже самое что 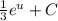$\frac{1}{3} e^u+C$ . Подставляем 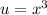u=x^3 и имеем 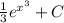$\frac{1}{3}e^{x^3}+C$ . Используем фундаментальную теорему исчисления:

$\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}$