Пусть длина палки равна 1. По условию задачи, если взять любые три кусочка, то сумма длин двух наименьших из них не больше длины самого длинного из них. Расположим кусочки в порядке убывания их длин: Требуется доказать, что Предположим противное, то есть что По условию При этом Идем по цепочке дальше. По условию , при этом . Продолжая этот процесс, получаем Суммируя, получаем Полученное противоречие (ведь сумма длин кусочков должна равняться 1) доказывает требуемое утверждение.
Замечание. Для тех, кто устал от этих выкладок - простое рассуждение без чисел. Первый (самый длинный кусок) лежит в первой трети отрезка [0;1]. Остаются две трети отрезка [0;1]. Пусть это отрезок [b;c]. Второй и третий куски лежат в его первой половине, а поскольку третий занимает не больше половины места, четвертый и пятый займут не больше половины от правой половины, и так далее. Сами додумайте до конца.
Пусть длина палки равна 1. По условию задачи, если взять любые три кусочка, то сумма длин двух наименьших из них не больше длины самого длинного из них. Расположим кусочки в порядке убывания их длин: Требуется доказать, что Предположим противное, то есть что По условию При этом Идем по цепочке дальше. По условию , при этом . Продолжая этот процесс, получаем Суммируя, получаем Полученное противоречие (ведь сумма длин кусочков должна равняться 1) доказывает требуемое утверждение.
Замечание. Для тех, кто устал от этих выкладок - простое рассуждение без чисел. Первый (самый длинный кусок) лежит в первой трети отрезка [0;1]. Остаются две трети отрезка [0;1]. Пусть это отрезок [b;c]. Второй и третий куски лежат в его первой половине, а поскольку третий занимает не больше половины места, четвертый и пятый займут не больше половины от правой половины, и так далее. Сами додумайте до конца.
Пусть длина палки равна 1. По условию задачи, если взять любые три кусочка, то сумма длин двух наименьших из них не больше длины самого длинного из них. Расположим кусочки в порядке убывания их длин: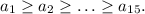
Требуется доказать, что 
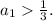Предположим противное, то есть что 
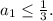По условию 
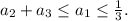При этом 
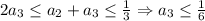Идем по цепочке дальше. По условию 
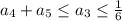, при этом 
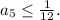. Продолжая этот процесс, получаем 
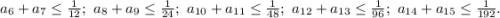Суммируя, получаем 
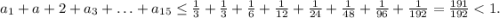Полученное противоречие (ведь сумма длин кусочков должна равняться 1) доказывает требуемое утверждение.
Замечание. Для тех, кто устал от этих выкладок - простое рассуждение без чисел. Первый (самый длинный кусок) лежит в первой трети отрезка [0;1]. Остаются две трети отрезка [0;1]. Пусть это отрезок [b;c]. Второй и третий куски лежат в его первой половине, а поскольку третий занимает не больше половины места, четвертый и пятый займут не больше половины от правой половины, и так далее. Сами додумайте до конца.
Пусть длина палки равна 1. По условию задачи, если взять любые три кусочка, то сумма длин двух наименьших из них не больше длины самого длинного из них. Расположим кусочки в порядке убывания их длин: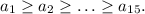
Требуется доказать, что 
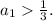Предположим противное, то есть что 
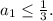По условию 
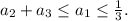При этом 
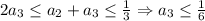Идем по цепочке дальше. По условию 
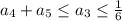, при этом 
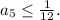. Продолжая этот процесс, получаем 
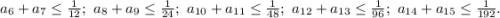Суммируя, получаем 
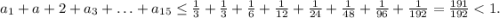Полученное противоречие (ведь сумма длин кусочков должна равняться 1) доказывает требуемое утверждение.
Замечание. Для тех, кто устал от этих выкладок - простое рассуждение без чисел. Первый (самый длинный кусок) лежит в первой трети отрезка [0;1]. Остаются две трети отрезка [0;1]. Пусть это отрезок [b;c]. Второй и третий куски лежат в его первой половине, а поскольку третий занимает не больше половины места, четвертый и пятый займут не больше половины от правой половины, и так далее. Сами додумайте до конца.