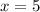Розв'язання завдання додаю
при
Пошаговое объяснение:
Выделим полный квадрат из выражения:
Квадрат любого числа - число неотрицательное
Причем равно 0 при
При умножении обеих частей неравенства на положительное число , знак неравенства не меняется
При вычитании одного и того же числа от обеих частей неравенства знак неравенства не меняется
значит, наименьшее значение выражения равно и достигается при
Розв'язання завдання додаю
Пошаговое объяснение:
Выделим полный квадрат из выражения:
Квадрат любого числа - число неотрицательное
Причем равно 0 при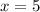
При умножении обеих частей неравенства на положительное число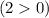 , знак неравенства не меняется
, знак неравенства не меняется
При вычитании одного и того же числа от обеих частей неравенства знак неравенства не меняется
значит, наименьшее значение выражения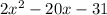 равно
равно 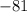 и достигается при
и достигается при