ответ:Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение.
Вся длина теплицы составляет 5 м = 500 см. Разделим эту длину на 80 см и округлим результат до ближайшего наибольшего целого, получим:
то есть, нужно заказать 7 дуг + 1 первая дуга = 8 дуг.
ответ: 8.
Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
Решение.
В теплице 3 грядки, между которыми будут дорожки, т.е. всего две дорожки. Длина каждой дорожки равна длине теплицы – 500 см, а ширина – 50 см. Площадь одной дорожки 500∙50 = 25000 см2, а двух – 2∙25000 = 50000 см2. Тротуарная плитка имеет размеры 25х25 см с площадью 625 см2. Следовательно, на дорожки необходимо
50000:625 = 80 плиток
Так как плитки продаются в упаковках по 6 штук, то необходимо купить
упаковок
(здесь - округление до ближайшего наибольшего целого).
ответ: 14.
Задание 3. Найдите высоту теплицы. ответ дайте в метрах с точностью до десятых.
Решение.
Высота теплицы определяется радиусом полуокружности длиной 6 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности . Для полуокружности она будет выглядеть так: , откуда
м
ответ: 1,9.
Задание 4. Найдите ширину узкой грядки, если ширина центральной грядки в полтора раза больше ширины узкой грядки. ответ дайте в сантиметрах с точностью до десятков.
Решение.
Условно представим теплицу с грядками: две по краям с шириной x см и одна центральная с шириной 1,5x см. Между ними дорожки шириной 50 см.
Учитывая, что вся ширина теплицы примерно 2R = 3,8 м = 380 см, получаем уравнение:
То есть, ширина узкой грядки равна 80 см.
ответ: 80.
Задание 5. Сколько квадратных метров плёнки необходимо купить для передней и задней стенок, если с учётом крепежа её нужно брать с запасом 10 %? ответ округлите до десятых.
Решение.
Передние и задние стенки двух полуокружностей образуют круг с радиусом R=1,9 м. Площадь такого круга, равна:
Игрок участвует хотя бы в одном из двух подряд идущих раундов. Игрок участвует в двух подряд идущих раундах при условии победы в первом из них.
Найдем общее число раундов:
Алиса участвовала в 10 раундах, соответственно, в 11 не участвовала.
Если Алиса не побеждала, то она участвовали либо во всех четных, либо во всех нечетных раундах. Так как она участвовала в 10 раундах, то значит это были четные раунды: 2, 4, ..., 20.
Предположим, что Алиса победила ровно 1 раз. Пусть это произошло в раунде . Тогда вместо участия в раундах , , ..., 20 из предыдущего условия она должна будет участвовать в раундах , , ..., 19. По нашему предположению в 19 раунде она также проиграет и будет участвовать в 21 раунде. Но тогда общее число раундов, в которых он участвовала будет равно 11. Противоречие. Значит, выиграть ровно 1 раз она не могла.
Аналогично, выиграть более одного раза она тем более не могла.
Значит, Алиса проиграла во всех своих раундах, в том числе и во втором.
ответ:Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение.
Вся длина теплицы составляет 5 м = 500 см. Разделим эту длину на 80 см и округлим результат до ближайшего наибольшего целого, получим:
то есть, нужно заказать 7 дуг + 1 первая дуга = 8 дуг.
ответ: 8.
Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
Решение.
В теплице 3 грядки, между которыми будут дорожки, т.е. всего две дорожки. Длина каждой дорожки равна длине теплицы – 500 см, а ширина – 50 см. Площадь одной дорожки 500∙50 = 25000 см2, а двух – 2∙25000 = 50000 см2. Тротуарная плитка имеет размеры 25х25 см с площадью 625 см2. Следовательно, на дорожки необходимо
50000:625 = 80 плиток
Так как плитки продаются в упаковках по 6 штук, то необходимо купить
упаковок
(здесь - округление до ближайшего наибольшего целого).
ответ: 14.
Задание 3. Найдите высоту теплицы. ответ дайте в метрах с точностью до десятых.
Решение.
Высота теплицы определяется радиусом полуокружности длиной 6 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности . Для полуокружности она будет выглядеть так: , откуда
м
ответ: 1,9.
Задание 4. Найдите ширину узкой грядки, если ширина центральной грядки в полтора раза больше ширины узкой грядки. ответ дайте в сантиметрах с точностью до десятков.
Решение.
Условно представим теплицу с грядками: две по краям с шириной x см и одна центральная с шириной 1,5x см. Между ними дорожки шириной 50 см.
Учитывая, что вся ширина теплицы примерно 2R = 3,8 м = 380 см, получаем уравнение:
То есть, ширина узкой грядки равна 80 см.
ответ: 80.
Задание 5. Сколько квадратных метров плёнки необходимо купить для передней и задней стенок, если с учётом крепежа её нужно брать с запасом 10 %? ответ округлите до десятых.
Решение.
Передние и задние стенки двух полуокружностей образуют круг с радиусом R=1,9 м. Площадь такого круга, равна:
м2
и с учетом +10% это будет:
м2
ответ: 12,5.
Пошаговое объяснение:
Игрок участвует хотя бы в одном из двух подряд идущих раундов. Игрок участвует в двух подряд идущих раундах при условии победы в первом из них.
Найдем общее число раундов:
Алиса участвовала в 10 раундах, соответственно, в 11 не участвовала.
Если Алиса не побеждала, то она участвовали либо во всех четных, либо во всех нечетных раундах. Так как она участвовала в 10 раундах, то значит это были четные раунды: 2, 4, ..., 20.
Предположим, что Алиса победила ровно 1 раз. Пусть это произошло в раунде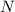
. Тогда вместо участия в раундах 
, 
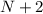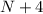, ..., 20 из предыдущего условия она должна будет участвовать в раундах 
, 
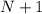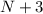, ..., 19. По нашему предположению в 19 раунде она также проиграет и будет участвовать в 21 раунде. Но тогда общее число раундов, в которых он участвовала будет равно 11. Противоречие. Значит, выиграть ровно 1 раз она не могла.
Аналогично, выиграть более одного раза она тем более не могла.
Значит, Алиса проиграла во всех своих раундах, в том числе и во втором.
ответ : Алиса