Рассмотрим события: А₁ - "первый попадет", A₂ - "второй попадет", B₁ - "первый не попадет", В₂ - "второй не попадет"
По условию:
События B₁ и В₂ противоположны по отношению к соответствующим событиям А₁ и A₂. Значит:
Для события E "один попадет в цель, а другой не попадет" есть два исхода:
С: "первый попадет, а второй не попадет"
D: "первый не попадет, а второй попадет"
Эти события несовместны (то есть не могут произойти одновременно), значит их вероятности будут складываться при определении общей вероятности.
Для события С должны выполниться два независимых события А₁ и В₂. Для события D должны выполниться два независимых события B₁ и A₂. Вероятности независимых событий перемножаются.
1) Вероятность выбрать первого мальчика равна . Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна . По теореме умножения, искомая вероятность:
2) Выбрать первую девочку можно с вероятностью . В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна . По теореме умножения, искомая вероятность:
3) Вероятность того, что среди двух выбранных человек окажутся девочка и мальчик, равна
Рассмотрим события: А₁ - "первый попадет", A₂ - "второй попадет", B₁ - "первый не попадет", В₂ - "второй не попадет"
По условию:
События B₁ и В₂ противоположны по отношению к соответствующим событиям А₁ и A₂. Значит:
Для события E "один попадет в цель, а другой не попадет" есть два исхода:
С: "первый попадет, а второй не попадет"
D: "первый не попадет, а второй попадет"
Эти события несовместны (то есть не могут произойти одновременно), значит их вероятности будут складываться при определении общей вероятности.
Для события С должны выполниться два независимых события А₁ и В₂. Для события D должны выполниться два независимых события B₁ и A₂. Вероятности независимых событий перемножаются.
Искомая вероятность:
В классе всего 12 + 18 = 30.
1) Вероятность выбрать первого мальчика равна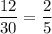 . Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна
. Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна 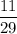 . По теореме умножения, искомая вероятность:
. По теореме умножения, искомая вероятность: 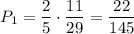
2) Выбрать первую девочку можно с вероятностью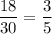 . В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна
. В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна 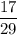 . По теореме умножения, искомая вероятность:
. По теореме умножения, искомая вероятность: 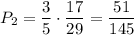
3) Вероятность того, что среди двух выбранных человек окажутся девочка и мальчик, равна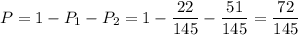
ответ: 1) 22/145; 2) 51/145; 3) 72/145.