936. На прямій позначено точки 0, A, B. Точка А лежить ліворуч від точки О на 15 клітинок, а точка B — праворуч від точки О на
5 клітинок. Скільки клітинок містить відрізок АВ? Як розміщена
точка О відносно точки: 1) А; 2) В?

желательно побыстрее(0(​

Найти объем треугольной пирамиды ABCD с вершинами A(2;-1;1), B(5;5;4), C(3;2;-1), D(4;1;3).

Решение находим с калькулятора.

Найти объем треугольной пирамиды ABCD с вершинами A(2;-1;1), B(5;5;4), C(3;2;-1), D(4;1;3).

Координаты векторов находим по формуле:

X = xj - xi; Y = yj - yi; Z = zj - zi

здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;

Например, для вектора AB

X = x2 - x1; Y = y2 - y1; Z = z2 - z1

X = 5-2; Y = 5-(-1); Z = 4-1

AB(3;6;3), AC(1;3;-2), AD(2;2;2), BC(-2;-3;-5), BD(-1;-4;-1), CD(1;-1;4).

Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:

Находим определитель матрицы: ∆ = 3 • (3 • 2-2 • (-2))-1 • (6 • 2-2 • 3)+2 • (6 • (-2)-3 • 3) = -18

(Если что это как пример так ты сможешь сделать это одно и тоже почти!)

Я докажу первое и последнее, остальное - сам.

1)

Доказательство "⇒".

Пусть у нас дано ((A∪B)⊂C), докажем тогда, что

1.1) A⊂C,

и

1.2) B⊂C.

1.1) x∈A⊂A∪B, ⇒ x∈A∪B⊂С, ⇒ x∈C. То есть A⊂C.

1.2) x∈B⊂A∪B, ⇒ x∈A∪B⊂C, ⇒ x∈C. То есть B⊂C.

чтд.

Доказательство "<=".

Пусть у нас дано: A⊂C и B⊂C. Докажем тогда, что

A∪B⊂C.

Пусть x∈A∪B, ⇔ x∈A или x∈B.

a) x∈A⊂C, ⇒ x∈C.

б) x∈B⊂C, ⇒ x∈C.

То есть A∪B⊂C.

чтд.

4)

Доказательство "⇒".

Пусть у нас дано (A⊂(B∪C)). Докажем тогда, что

Пусть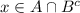 , ⇔ 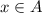и , ⇔

и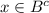

Тогда т.к. A⊂B∪C, имеем

и

Первый случай. Если x∈B и x∉B, то x∈∅⊂C ⇒ x∈C.

Второй случай. Если x∈C и x∉B, то x∈C\B⊂C, ⇒ x∈C.

чтд.

Доказательство "<=".

Пусть у нас дано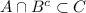 , докажем тогда, что

A⊂ B∪C.

Пусть x∈A. Тут возможны два варианта x∈B, либо x∉B.

Случай первый: x∈A и x∈B, ⇒ x∈A∩B⊂B, ⇒ x∈B⊂B∪C, ⇒ x∈B∪C.

Случай второй: x∈A и x∉B, ⇒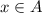 и , ⇒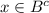

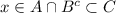⇒ , ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.

чтд.