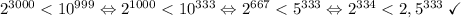98 ! заранее !
а). представьте число 100 в виде суммы нескольких натуральных чисел так, чтобы их произведение было наибольшим. и докажите, что большее произведение получить нельзя.
б). перемножили три тысячи двоек. докажите, что в записи получившегося числа:
не более 1000 цифр и не менее 900 цифр.

а)Пусть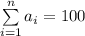 , при этом 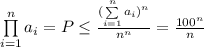; Пусть 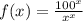, тогда 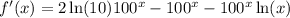; Экстремум находится в точке 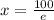; ; 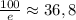Поэтому при 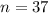достигается максимум, т.е. 100 должно быть представлено в виде 37-ми слагаемых. А, значит, каждое из слагаемых либо 3, либо 2. Значит, искомое произведение есть число вида 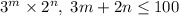. 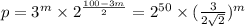, поэтому чем больше m, тем лучше (возраст. функция). Стало быть, m=32, а искомый набор: 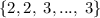- 32 тройки и две двойки.

б) Нужно доказать неравенства: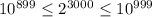

Покажем справедливость первого: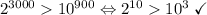  

Теперь второго: