Последовательность стремится к нулю, поэтому исходная последовательность стремится к нулю по лемме о "двух правоохранителях" (милиционерах, полицейских, жандармах, копах и т.д - в зависимости от страны и эпохи).
Доказать, что можно многими (с правила Лопиталя, теоремы Штольца, бинома Ньютона, неравенства Бернулли - кто подскажет еще ?).
Например, бином Ньютона дает нам следующую оценку:
.
Неравенство Бернулли применяем так:
Лопиталь заменяет n на x, проверяет наличие неопределенности
вычисляет предел отношения производных:
и поскольку предел отношения производных существует и равен нулю, исходный предел также равен нулю.
Штольц не так хорошо известен, но наш предел вычисляет мгновенно. Однако я устал и (возможно) утомил читателя. Поэтому, памятуя Козьму Пруткова, заканчиваю.
1)CB - ребро двугранного угла. Чтобы найти линейный угол двугранного угла, необходимо построить плоскость ⊥ ребру BC. Опустим AE ⊥ BC, DE ⊥ BC по теореме о трех перпендикулярах, где AE - проекция, DE - наклонная. BC - прямая проведенная через основание наклонной и перпендикулярная проекции. AE и DE - находятся в одной плоскости и пересекаются, ВС - перпендикулярна AE и DE ⇒ перпендикулярна плоскости AED ⇒∠AED - линейный угол двугранного угла ∠ABCD. 2) ΔABC - равнобедренный, т.к. AB = AC = 10 см ⇒ опущенный перпендикуляр AE есть медиана ⇒ EC = DC/2 = 6 см. 3) ΔAEC - прямоугольный По т. Пифагора (см) 4) т.к. AD = AE = 8(см) ⇒ ΔADE равнобедренный. ΔADE - прямоугольный и равнобедренный ⇒ ∠AED = 45° ответ: ∠AED = 45°
Последовательность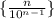 стремится к нулю, поэтому исходная последовательность стремится к нулю по лемме о "двух правоохранителях" (милиционерах, полицейских, жандармах, копах и т.д - в зависимости от страны и эпохи).
стремится к нулю, поэтому исходная последовательность стремится к нулю по лемме о "двух правоохранителях" (милиционерах, полицейских, жандармах, копах и т.д - в зависимости от страны и эпохи).
Доказать, что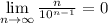 можно многими (с правила Лопиталя, теоремы Штольца, бинома Ньютона, неравенства Бернулли - кто подскажет еще ?).
можно многими (с правила Лопиталя, теоремы Штольца, бинома Ньютона, неравенства Бернулли - кто подскажет еще ?).
Например, бином Ньютона дает нам следующую оценку:
Неравенство Бернулли применяем так:
Лопиталь заменяет n на x, проверяет наличие неопределенности
Штольц не так хорошо известен, но наш предел вычисляет мгновенно. Однако я устал и (возможно) утомил читателя. Поэтому, памятуя Козьму Пруткова, заканчиваю.
Чтобы найти линейный угол двугранного угла, необходимо построить плоскость ⊥ ребру BC.
Опустим AE ⊥ BC, DE ⊥ BC по теореме о трех перпендикулярах, где AE - проекция, DE - наклонная. BC - прямая проведенная через основание наклонной и перпендикулярная проекции.
AE и DE - находятся в одной плоскости и пересекаются, ВС - перпендикулярна AE и DE ⇒ перпендикулярна плоскости AED ⇒∠AED - линейный угол двугранного угла ∠ABCD.
2) ΔABC - равнобедренный, т.к. AB = AC = 10 см ⇒ опущенный перпендикуляр AE есть медиана ⇒ EC = DC/2 = 6 см.
3) ΔAEC - прямоугольный
По т. Пифагора
4) т.к. AD = AE = 8(см) ⇒ ΔADE равнобедренный.
ΔADE - прямоугольный и равнобедренный ⇒ ∠AED = 45°
ответ: ∠AED = 45°