А 3. По данным рисунка вычислить
отметку точки с.
= 06I2. с= 0827. B = 1158
7 I
C
B
А
1= 32370

Показать ответ

Ответ:

bondarantona

07.04.2022 20:11

1) Y - центральный и X - вписанный углы

Центральный угол равен дуге на которую он опирается, вписанный же половине

X=60 градусов, Y=120 градусов

2) синус угла равен отношению противолежащей стороны к гипотенузе, из рисунка это отношение 3/5=0,6

3) По равенству сторон заметно что искоемое значение является средней линией треугольника, а так как средняя линяя равна половине основания, то x=4

4) Это египетский треугольник со сторонами 3 4 5, x=4

Можно найти по теореме пифагора a^2=c^2-b^2= 25 - 9 = 16, откуда x=4

5) Площадь параллелограмма равна произведению основания на высоту, проведенную к нему S=ah=3*8=24

6) Противоположные углы параллелограмма равны, откуда Y=54 градуса

X = (360-54*2)/2 = 126

7) Обе стороны меньше соотвествующих вдважды 12/6=2 8/4=2, коэффециент подобия равен 2

8) Это параллелограмм, противоположные углы равны, значит 150, остальные два угла 180-150=30

По рисунку видно, что x половина угла x=30/2=15

Вторая часть

1) Радиус описанной окружности равен R=abc/4S из формулы площади треугольника через радиус вписанной окружности S=abc/4R

Найдем гипотенузу по формуле Пифагора c^2=a^2+b^2=144+256=400, откуда c=20

R= (20*16*12) / ( 4 * 0,5 * 12 * 16) = 10, ответ Б

2) Пусть x меньшая, 3x большая сторона, периметр палллелограмма равен P=2ab

2*(3x+x)=60

8x=60 x=7,5 3x=22,5, ответ Б

3) составим уравнение, пусть x неизвестный катет, x+8 гипотенуза. По теореме Пифагора:

20^2 + x^2 = (x+8)^2

400 + x^2 = x^2 + 16x + 64

16x = 336

x=21 x+8=29

P = 20+21+29 = 70, ответ В

4) пусть диагональ BD=12, диагональ AC=4√3

Диагонали ромба деляет его на 4 прямоугольных треугольника, при этом катеты равны половине диагоналей и гипотенуза равна стороне ромба.

BO=OD=6

AO=OC=2√3

AB^2=AO^2+OB^2=36+12=48=4√3

AO=1/2AB ⇒ угол ABO=30 градусов, а угол BAO=180-90-30=60

тогда угол B=2ABO=30*2=60, а угол A=2BAO=60*2=120

0,0(0 оценок)

Ответ:

aki4

09.12.2021 13:46

Из знаменателя нам нужно только взять ограничение подкоренного выражения, которое и будет являться областью определения неравенства (в числителе ограничений нет):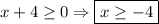 $x+4\geq 0 \Rightarrow \boxed{x\geq -4}$

Помним про это.

Теперь решаем само неравенство

$\displaystyle 26^{|x|}=(2\cdot 13)^{|x|}=2^{|x|}\cdot 13^{|x|}$ - это нам потребуется

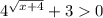Заметим, что $\displatstyle 4^{\sqrt{x+4}}+3 0$ для любых , поэтому умножим все неравенство на знаменатель и ничего не поменяется, избавимся от дроби. И сразу запишем в числителе то, что уже преобразовали.

$\displaystyle 2^{|x|}\cdot 13^{|x|}-2^{|x|}-2\cdot 13^{|x|}+2\geq 0 ;\ 13^{|x|}(2^{|x|}-2)-(2^{|x|}-2)\geq 0; \\ (2^{|x|}-2)(13^{|x|}-1)\geq 0$

Чтобы решить полученное неравенство методом интервалов, найдем нули выражения, стоящего левее знака:

$\displaystyle \\ (2^{|x|}-2)(13^{|x|}-1)= 0 \Leftrightarrow \left [ {{2^{|x|}-2=0} \atop {13^{|x|}-1=0} \right. \Rightarrow \left [ {{2^{|x|}=2^1} \atop {13^{|x|}}=13^0} \right. \Rightarrow \\ \left [ {{|x|=1} \atop {|x|=0}} \right. \Rightarrow \left [ {{x=\pm1} \atop {x=0}} \right.$

Замечательно, теперь ничего не мешает использовать метод интервалов. Заметим, что функция, у которой мы нули находили - четная, так как везде с иксами модули стоят, поэтому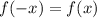 f(-x)=f(x) , и нули тоже симметричны. То есть можно найти знаки на положительных значениях, а на отрицательных симметрично относительно нуля расставить.

На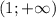 $(1;+\infty)$ обе скобки при подстановке какого-либо числа положительны, все выражение положительно (+).

На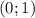 (0;1) (можно взять как пример 0.5, так как это степень, это будет корень второй степени, то есть обычный корень) вот что получается:

$(\sqrt{2}-2)(\sqrt{13}-1)$ , первая скобка отрицательна, вторая положительна, то есть выражение отрицательно (-).

Теперь симметрично отображаем и получаем на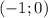 (-1;0) отрицательно (-)

А на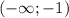 $(-\infty; -1)$ положительно (+).

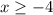
То есть надо было бы взять $x\in(-\infty;-1]\cup \{0\} \cup [1;+\infty)$ , не забываем брать сами нули, так как неравенство нестрогое, но вспомним про ограничение из знаменателя, которое $x\geq -4$