Возможно это то, что вам нужно. Системы автоматических устройств выполняют функцию управления, регулирования, контроля и защиты как технологических процессов, так и машин, оборудования и системы в целом. Развитие техники в строительном производстве идет по пути максимальной механизации и автоматизации производственных процессов. Образцами широкой автоматизации технологических процессов в строительном производстве являются автоматизированные заводы по производству бетона, железобетонных конструкций и др. Элементы автоматических устройств, применяемых в автоматических системах, могут быть электрическими, пневматическими и гидравлическими. Современное автоматическое устройство включает в себя датчики, дистанционные передачи, преобразователи, реле, измерительные приборы и исполнительные органы. В простых автоматических устройствах некоторые из этих элементов (например, дистанционная передача, измерительные приборы и др.) могут отсутствовать. Наиболее сложной функцией автоматики является автоматическое регулирование, состоящее в поддержании без участия человека на постоянном уровне величин, определяющих протекание технологического процесса. Объект, в котором процесс в той или иной мере автоматически регулируется, называется регулируемым объектом, а величины, подлежащие регулированию,— регулируемыми параметрами. Регулировать можно один или несколько параметров объекта регулирования. Выбранный для конкретных условий автоматический регулятор должен поддерживать в определенных пределах величину и продолжительность отношения регулируемого параметра, т. е. обеспечить устойчивое регулирование. Устойчивым является регулирование, плавно изменяющее регулируемый параметр либо без колебаний, либо с небольшими затухающими колебаниями. По назначению различают регуляторы расхода, давления, температуры и т. д. По действия автоматические регуляторы подразделяются на непосредственного действия, в которых усилие, необходимое для перемещения регулирующего органа, создается изменением регулируемого параметра без применения постороннего источника энергии, и непрямого (косвенного) действия, работающие с использованием постоянного источника энергии. Регуляторы делятся также на регуляторы прерывного и непрерывного действия. В прерывном случае регулятор или его связь с регулирующим органом включается периодически, во втором — непрерывно воздействует на регулирующий орган до тех пор, пока регулируемая величина не совпадет с заданным значением. Регулируемый объект вместе с присоединенным к нему автоматическим регулятором называется системой автоматического регулирования (САР). Система автоматического регулирования является замкнутой системой, в которой отключения регулируемой величины от заданного значения преобразуются автоматически в воздействие на регулирующий орган. Характерной особенностью большинства автоматических устройств является наличие обратной связи. Обнаружив отклонение регулируемой величины от требуемого значения, чувствительный элемент регулятора посылает командный импульс к регулирующему органу, который уменьшает или увеличивает перемещение рабочего органа. Сигнализирующие устройства автоматических устройств могут быть выполнены со звуковыми, световыми и электромагнитными сигналами. Для звуковых сигналов используются звонки, гудки и сирены, для световых — электрические лампочки, для электромагнитных сигнальных реле — бленкеры. При подаче тока в катушку бленкера выпадает сигнализирующая пластинка — флажок. С перечисленных устройств сигнализируется либо включение и отключение тех или иных агрегатов, либо состояние их неисправности. Блокировка в автоматических устройствах служит для предотвращения подключения механизмов в непредусмотренное время. Устройства для блокировки бывают электрические, механические, пневматические и гидравлические. В автоматизированных устройствах наиболее широко применяется электрическая блокировка. В частности, в электроприводах она служит для обеспечения определенных переключений или последовательности пуска и остановки механизмов, связанных межу собой общей технологической зависимостью. Под блокировкой механизмов и устройств понимается такая электрическая или механическая связь между их пусковыми аппаратами, которая ставит в зависимость действие одного механизма или устройства от другого. В строительном производстве часто используются группы транспортеров, требующих согласованной работы. Работа транспортеров связывается между собой, а иногда, в зависимости от необходимости, также и с работой других механизмов. Эти связи осуществляются целым рядом электрических блокировочных цепей. В целях предотвращения возможных завалов в случае непредвиденной остановки одного из транспортеров должна быть обеспечена автоматическая остановка всех транспортеров, предшествующих ему по ходу потока.
Математическое ожидание - сумма попарных произведений значений случайной величины на вероятности, с которыми эти величины достигаются.
То есть, если значение достигается с вероятностью , значение - с вероятностью , и так далее, значение - с вероятностью , то математическое ожидание:
Математическое ожидание показывает среднее или наиболее вероятное значение случайной величины. В единичном испытании математическое ожидание равно вероятности события.
Для вычисления мат.ожидания как ожидаемого числа вопросов используем формулу:
, где - вероятность осуществления некоторого события, - число повторений.
В нашем случае, - вероятность того, что очередной вопрос не из группы "спринт", - число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
Поскольку вопросов не из группы "спринт" , а общее число вопросов , то вероятность того, что очередной вопрос не из группы "спринт" равна:
Число вопросов группы "спринт":
Тогда:
Конечно, можно действовать по первой формуле.
Для этого рассмотрим возможные количества вопросов не из группы "спринт", которые могли оказаться в группе "спринт". Это количества: 0, 1, 2, ..., 17, 18.
Найдем вероятности осуществления этих возможностей. Так как общий смысл сохраняется во всех ситуациях, то рассмотрим нахождение вероятности в общем виде - найдем с какой вероятностью i вопросов не из группы "спринт" попадут в группу "спринт".
Число выбрать вопросы в группу "спринт" с учетом этого условия соответствует тому, что из 18 вопросов не группы "спринт" мы выберем некоторые i штук, а остальные (30-i) штук мы выберем из 30 вопросов группы "спринт". Итоговое число благоприятных комбинаций: .
Общее число выбрать вопросы в группу "спринт" соответствует тому, что из всех 48 вопросов мы выберем некоторые 30 штук. Общее число комбинаций: .
Тогда, ситуации, что в группе "спринт" окажется i вопросов не из группы "спринт", соответствует вероятность .
Запишем математическое ожидание как сумму попарных произведений значений на вероятность:
Можно попробовать упростить эту формулу:
Далее нужно каким-либо досчитать эту величину. Вычисления дают полученный ранее результат:
Учитывая контекст вопроса, а именно, что мат.ожидание соответствует числу вопросов, попавших в группу "спринт", запишем также округленное до целого числа значение мат.ожидания:
Математическое ожидание - сумма попарных произведений значений случайной величины на вероятности, с которыми эти величины достигаются.
То есть, если значение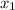 достигается с вероятностью
достигается с вероятностью 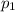 , значение
, значение  - с вероятностью
- с вероятностью  , и так далее, значение
, и так далее, значение 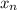 - с вероятностью
- с вероятностью 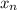 , то математическое ожидание:
, то математическое ожидание:
Математическое ожидание показывает среднее или наиболее вероятное значение случайной величины. В единичном испытании математическое ожидание равно вероятности события.
Для вычисления мат.ожидания как ожидаемого числа вопросов используем формулу:
В нашем случае, - вероятность того, что очередной вопрос не из группы "спринт",
- вероятность того, что очередной вопрос не из группы "спринт", 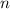 - число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
- число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
Поскольку вопросов не из группы "спринт"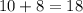 , а общее число вопросов
, а общее число вопросов  , то вероятность того, что очередной вопрос не из группы "спринт" равна:
, то вероятность того, что очередной вопрос не из группы "спринт" равна:
Число вопросов группы "спринт":
Тогда:
Конечно, можно действовать по первой формуле.
Для этого рассмотрим возможные количества вопросов не из группы "спринт", которые могли оказаться в группе "спринт". Это количества: 0, 1, 2, ..., 17, 18.
Найдем вероятности осуществления этих возможностей. Так как общий смысл сохраняется во всех ситуациях, то рассмотрим нахождение вероятности в общем виде - найдем с какой вероятностью i вопросов не из группы "спринт" попадут в группу "спринт".
Число выбрать вопросы в группу "спринт" с учетом этого условия соответствует тому, что из 18 вопросов не группы "спринт" мы выберем некоторые i штук, а остальные (30-i) штук мы выберем из 30 вопросов группы "спринт". Итоговое число благоприятных комбинаций: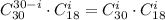 .
.
Общее число выбрать вопросы в группу "спринт" соответствует тому, что из всех 48 вопросов мы выберем некоторые 30 штук. Общее число комбинаций: .
.
Тогда, ситуации, что в группе "спринт" окажется i вопросов не из группы "спринт", соответствует вероятность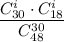 .
.
Запишем математическое ожидание как сумму попарных произведений значений на вероятность:
Можно попробовать упростить эту формулу:
Далее нужно каким-либо досчитать эту величину. Вычисления дают полученный ранее результат:
Учитывая контекст вопроса, а именно, что мат.ожидание соответствует числу вопросов, попавших в группу "спринт", запишем также округленное до целого числа значение мат.ожидания:
ответ: