0,8+3/7= 8/10 + 3/7 = 4/5+ 3/7 =1 8/35 (десятичную дробь переводим в обыкновен.для просоты сократим на 2 и решаем)
26 1/11 -5,7 =26 1/11- 5 7/10 = 25 (1/11+11/11)-5 7/10=(25-2)+(12/11-7/10)= 20+ (120-77/110)= 20 43/110 (объясняю:от26 целых занимаем 1 целую и добавяляем ее к дробной части (11/11+1/11=12/11). Таким образом : вычитаем сначала целые части чисел (25-5=20целых) +(12/11-7/10) общий знаменатель 110 в числителе получаем (12*10-7*11=43 таким образом при вычитании дробной части получили 43/110)
1. На первое место можно использовать 6 цифр, на второе место - оставшиеся 5 цифр, на третье место - оставшиеся 4 цифр, на четвертое место - 3 цифры, на пятое место - 2 цифры, на последнее место - одна оставшаяся цифра. По правилу произведения, составить шестизначных чисел можно
2. Порядок выбора учащихся не имеет значения, поэтому выбрать двух учащихся для участия в городской олимпиаде можно
3. Дежурного можно выбрать а его По правилу произведения это можно сделать.
4. Всего всевозможных элементарных исходов 30 из них благоприятствуют только 30-5=25 элементарных исходов, т.е.
m = 25
n = 30
Вероятность того, что она не окажется учебником, равна 25/30 = 5/6
5. Выбрать две книги можно а три журнала - По правилу произведения можно сделать этот выбор.
6. Всего всевозможных элементарных исходов: 5! = 120 слов из них благоприятствуют только два слова: "конус" или "сукно".
n = 120
m = 2
Вероятность того, что в результате получится слово "конус" или "сукно", равна 2/120 = 1/60
26 1/11 -5,7 =26 1/11- 5 7/10 = 25 (1/11+11/11)-5 7/10=(25-2)+(12/11-7/10)=
20+ (120-77/110)= 20 43/110
(объясняю:от26 целых занимаем 1 целую и добавяляем ее к дробной части (11/11+1/11=12/11). Таким образом : вычитаем сначала целые части чисел (25-5=20целых) +(12/11-7/10) общий знаменатель 110 в числителе получаем (12*10-7*11=43 таким образом при вычитании дробной части получили 43/110)
1. На первое место можно использовать 6 цифр, на второе место - оставшиеся 5 цифр, на третье место - оставшиеся 4 цифр, на четвертое место - 3 цифры, на пятое место - 2 цифры, на последнее место - одна оставшаяся цифра. По правилу произведения, составить шестизначных чисел можно
2. Порядок выбора учащихся не имеет значения, поэтому выбрать двух учащихся для участия в городской олимпиаде можно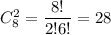
3. Дежурного можно выбрать а его По правилу произведения это можно сделать.
4. Всего всевозможных элементарных исходов 30 из них благоприятствуют только 30-5=25 элементарных исходов, т.е.
m = 25
n = 30
Вероятность того, что она не окажется учебником, равна 25/30 = 5/6
5. Выбрать две книги можно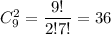 а три журнала -
а три журнала - 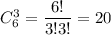 По правилу произведения можно сделать этот выбор.
По правилу произведения можно сделать этот выбор.
6. Всего всевозможных элементарных исходов: 5! = 120 слов из них благоприятствуют только два слова: "конус" или "сукно".
n = 120
m = 2
Вероятность того, что в результате получится слово "конус" или "сукно", равна 2/120 = 1/60