Дано: цилиндр, осевое сечение ABCD, площадь осевого сечения S(ABCD) = 16 см², площадь основания Sосн = 8 см².
Найти: высоту цилиндра H, площадь боковой поверхности цилиндра Sбок.
Решение.
Осевым сечением цилиндра называется сечение, проходящее через ось цилиндра. Оно представляет собой прямоугольник, две стороны которого образующие цилиндра, а две другие - диаметры оснований цилиндра.
На чертеже OD = R - радиус основания, AD =2R - диаметр основания, CD = H - высота цилиндра.
1) Зная площадь основания (площадь круга), найдем радиус и диаметр основания:
Sосн = πR² = 8 см². ⇒ ;
Диаметр основания ;
2) Площадь сечения цилиндра - это площадь прямоугольника ABCD.
S(ABCD) = AD * CD = D * H = 16 см².
;
Высота цилиндра см.
3) Боковая поверхность цилиндра равна произведению длины окружности основания на высоту цилиндра.
Высота цилиндра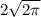 см.
см.
Боковая поверхность цилиндра см².
см².
Пошаговое объяснение:
Дано: цилиндр, осевое сечение ABCD, площадь осевого сечения S(ABCD) = 16 см², площадь основания Sосн = 8 см².
Найти: высоту цилиндра H, площадь боковой поверхности цилиндра Sбок.
Решение.
Осевым сечением цилиндра называется сечение, проходящее через ось цилиндра. Оно представляет собой прямоугольник, две стороны которого образующие цилиндра, а две другие - диаметры оснований цилиндра.
На чертеже OD = R - радиус основания, AD =2R - диаметр основания, CD = H - высота цилиндра.
1) Зная площадь основания (площадь круга), найдем радиус и диаметр основания:
Sосн = πR² = 8 см². ⇒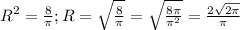 ;
;
Диаметр основания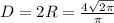 ;
;
2) Площадь сечения цилиндра - это площадь прямоугольника ABCD.
S(ABCD) = AD * CD = D * H = 16 см².
Высота цилиндра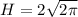 см.
см.
3) Боковая поверхность цилиндра равна произведению длины окружности основания на высоту цилиндра.
Длина окружности основания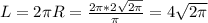 ;
;
Sбок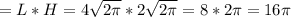 см².
см².