1. Найди среди этих слов величины: масса, цвет, длина, запах, объем, аппетит, время, температура.Чтобы измерить величину, надо выбрать мерку и узнать, сколько раз она содержится в величине. Мерка измерения — это единица измерения.На нашем интернет-уроке мы познакомимся с величинами: длина, масса, площадь и объём. О времени мы говорили здесь Интернет-урок по математике «Время. Единицы измерения времени»Величина — длинаВ каких случаях мы измеряем длину?…. Верно, расстояние между городами, рост человека, длина стола (чтобы купить для него скатерть), ткань, чтобы хватило на пошив одежды и т.д.Меры, или единицы измерения, длины — это миллиметр, сантиметр, дециметр, метр и километр.Самая маленькая единица измерения — миллиметр. Сантиметр ты можешь увидеть на школьной линейке. Самая большая единица измерения — это километр.Единицу измерения мы выбирает ту, которая лучше всего подходит для измерения данного предмета.Если ты будешь измерять расстояние между городами для своего путешествия, ты возьмёшь самую большую единицу измерения — километр.Если ты будешь делать поделку по технологии и тебе надо вырезать из бумаги шаблон, ты будешь использовать единицу измерения — сантиметр.А вот в древности, мерой длины всегда был человек. Система древнерусских мер длины включала в себя следующие основные меры:
Докажем, что если после случайного распределения участков ни одному из дачников не достался лучший на его взгляд участок (*), то возможно перераспределить участки так, чтобы каждому достался более хороший на его взгляд участок. В условии же сказано, что распределение оказалось таково, что при любом другом, хотя бы одному достался бы более плохой участок. Если мы докажем вышеизложенное утверждение, то по противоречию будет следовать, что распределение не отвечает условию (*), а значит задача решена.
Рассмотрим таблицу , где за строками скрываются дачники, а за столбцами - участки. В пересечении строки и столбца будет стоять число , которое равно месту, которое отдал i-ый дачник j-ому участку.
Пусть произошло распределение по условию (*). Пусть i-ому участнику достался участок с местом (на его взгляд) i; Тогда существует участок, который лучше того, который ему достался. Аналогично для остальных дачников. Для того, чтобы перераспределить участки необходимо, чтобы сумма всех участков, которые лучше того, что достались дачнику была не меньше общего количества дачников (иначе были бы пересечения и на один участок претендовало бы не менее двух дачников). То есть ; Так как никому не досталось первое место, а у каждого место не выше второго, то действительно сумма мест не меньше удвоенного количества дачников. Неравенство справедливо, а, значит, задача решена
Докажем, что если после случайного распределения участков ни одному из дачников не достался лучший на его взгляд участок (*), то возможно перераспределить участки так, чтобы каждому достался более хороший на его взгляд участок. В условии же сказано, что распределение оказалось таково, что при любом другом, хотя бы одному достался бы более плохой участок. Если мы докажем вышеизложенное утверждение, то по противоречию будет следовать, что распределение не отвечает условию (*), а значит задача решена.
Рассмотрим таблицу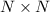
, где за строками скрываются дачники, а за столбцами - участки. В пересечении строки и столбца будет стоять число 
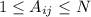, которое равно месту, которое отдал i-ый дачник j-ому участку.
Пусть произошло распределение по условию (*). Пусть i-ому участнику достался участок с местом (на его взгляд) i; Тогда существует
участок, который лучше того, который ему достался. Аналогично для остальных дачников. Для того, чтобы перераспределить участки необходимо, чтобы сумма всех участков, которые лучше того, что достались дачнику была не меньше общего количества дачников (иначе были бы пересечения и на один участок претендовало бы не менее двух дачников). То есть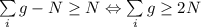 
; Так как никому не досталось первое место, а у каждого место не выше второго, то действительно сумма мест не меньше удвоенного количества дачников. Неравенство справедливо, а, значит, задача решена