Андрей вышел из школы и направился к школе со скоростью 80м/мин. через 10 мин. после выхода андрея к бассейну из школы отправился борис, скорость которого на 20 м/мин. больше, чем скорость андрея. через сколько минут после своего выхода андрей встретил бориса, если расстояние между школой и бассейном равно 1 км. 700 м?
В первой стопке 40 журналов, а во второй — 30.
Пошаговое объяснение:
Если бы в первой стопке было бы столько же журналов сколько и во второй, то сумма журналов была бы:
70 - 10 = 60 — общее количество журналов в двух одинаковых стопках.
Таким образом мы уравняли количество журналов в обеих стопках. Теперь, разделив 60 на количество стопок, можно узнать сколько журналов во второй стопке:
60 : 2 = 30 журналов.
Чтобы узнать, сколько журналов в первой стопке, надо вернуть обратно 10 журналов в первую стопку:
30 + 10 = 40 журналов.
Решение задачи по действиям можно записать так:
1) 70 - 10 = 60 — общее количество журналов в двух одинаковых стопках.
2) 60 : 2 = 30 — количество журналов во второй стопке.
3) 30 + 10 = 40 — количество журналов в первой стопке.
Можно выполнить проверку и убедиться, что задача решена правильно:
40 + 30 = 70 — общее количество журналов,
40 - 30 = 10 — разница в количестве журналов между стопками.
Пошаговое объяснение:
Общую схему рассмотрим в примере 1) 2,1(6).
Пусть число а,b(c) периодичное, где а - целая часть, b - число в предпериоде, c - число в периоде, в нашем примере а=2, b=1, c=6. Чтобы преобразовать эту дробь в обыкновенную нужно придерживаться следующему правилу:
а) Считаем количество цифр в периоде десятичной дроби и обозначаем количество цифр через k, в нашем примере k=1, так как число 6 состоит из одной цифры;
б) Считаем количество цифр, стоящих в предпериоде, то есть количество цифр, стоящих после запятой, но до периода десятичной дроби и обозначаем количество цифр через m, в нашем примере m=1, так как число 1 состоит из одной цифры;
в) Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа , в нашем примере n=16;
г) Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа , в нашем примере s=1;
д) Подставляем найденные значения в формулу
Нетрудно видеть, что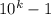
состоит из k цифр 9, а 
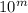из m цифр 0 после 1.
В нашем примере
2) 5,14(33) ⇒ a=5, k=2, m=2, n=1433, s=14. Тогда
3) 0,11(35) ⇒ a=0, k=2, m=2, n=1135, s=11. Тогда
4) 0,214(45) ⇒ a=0, k=2, m=3, n=21445, s=214. Тогда