Математика: Ar ctg y=y^3+9x похідна неявно заданої функції

Ar ctg y=y^3+9x похідна неявно заданої функції

Показать ответ

Ответ:

asyazakharchenko3011

27.10.2020 18:05

2cos^2x+9|sinx|-6=0

Раскрываем знак модуля:

$\left \{ {{sinx\geq 0} \atop {2cos^2x+9sinx -6=0}} \right.$ или $\left \{ {{sinx< 0} \atop {2cos^2x-9sinx -6=0}} \right.$

Решаем уравнения в каждой системе:

2(1-sin^2x)+9sinx-6=0 или 2(1-sin^2x)-9sinx-6=0

2sin^2x-9sinx+4=0 или 2sin^2x+9sinx+4=0

D=81-4·2·4=49

$sinx=\frac{1}{2}$ или sinx=4 или $sinx=-\frac{1}{2}$ или sinx=-4

|sinx| ≤ 1

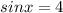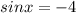Уравнения sinx=4 и sinx=-4 не имеют корней.

$sinx=\frac{1}{2}$ удовл условию sinx≥0 и $sinx=-\frac{1}{2}$ удовл условию sinx < 0

$x=(-1)^{k}\frac{\pi }{6}+\pi k, k \in Z$ $x=(-1)^{n}(-\frac{\pi }{6})+\pi n, n \in Z$

$x=-\frac{\pi }{6} ; x=\frac{\pi }{6} ; x=\frac{5\pi }{6}$ - корни, принадлежащие отрезку $(-\frac{\pi }{2};\pi)$

Пусть х кг свинца было в сплаве, тогда процентное содержание меди:

$\frac{30}{x+30}\cdot 100$ %

В новом сплаве ( х+10) кг свинца и 30 кг меди.

Тогда процентное содержание меди:

$\frac{30}{x+10+30}\cdot 100$ %

По условию: процентное содержание меди уменьшилось на 10%

$\frac{30}{x+10+30}\cdot 100=0,9\cdot \frac{30}{x+30}\cdot 100$

$\frac{30}{x+40}= \frac{27}{x+30}$

30(x+30)=27(x+40)

30x+900=27x+1080

3x=180

x=60

60 кг было в сплаве

60+10=70 кг стало в сплаве

О т в е т. 70 кг

0,0(0 оценок)

Ответ:

elvinabilalova

27.10.2020 18:05

11. 1) х∈(-π/2;0); IsinxI=-sinx; 2*(1-sin²x)-9sinx-6=0; -2sin²x+2-9sinx-6=0

2sin²x+9sinx+4=0; sinx=(-9±√(81-32))/4; sinx=(-9±7))/4; sinx=-4; ∅, т.к. IsinxI≤1; sinx=-1/2; х=(-1)ⁿ⁺¹π/6+πn; n∈Z; Если n=0, то х= -π/6, если n=1, то х= 5π/6, но 5π/6∉(-π/2;0), если n=-1, то х= -5π/6∉(-π/2;0);

2) х∈(0;π); IsinxI=sinx; 2*(1-sin²x)+9sinx-6=0; -2sin²x+2+9sinx-6=0

2sin²x-9sinx+4=0; sinx=(9±√(81-32))/4; sinx=(9±7))/4; sinx=4; ∅, т.к. IsinxI≤1; sinx=1/2; х=(-1)ⁿπ/6+πn; n∈Z; Если n=0, то х= π/6, если n=1, то х= 5π/6, но 5π/6 ∈(0;π), если n=-1, то х= -7π/6∉(0;π);

3) если х=0, то IcosxI=√3, что невозможно, поэтому

ответ : ±π/6; 5π/6

12. х кг цинка было в сплаве, процентное содержание меди в нем составляло 30*100%/(х+30),

Новый сплав содержал ( х+10) кг цинка и 30 кг меди; процентное содержание меди в нем 30*100%/(х+10+30)=30*100%/(х+40),

После понижения процентного содержания на 10%, в нем стало 90% меди, и тогда 30*100%/(х+30)=0.9*30*100%/(х+40);

x+30=0.9*(x+40)

x+30=0.9*x+36

0.1х=6; х=60; 60 кг в сплаве цинка было, а стало 60+10=70/кг/

ответ 70 кг.

0,0(0 оценок)

Популярные вопросы: Математика