Написать уравнение касательной и нормали к графику функции f(x)=x^4/4-27x+60 в точке х₀=2.
Уравнение касательной имеет вид y=48-19x.
Уравнение нормали имеет вид y=188/19+х/19.
Вспомним общий вид уравнения касательной:
И общий вид уравнения нормали:
Для этого в функцию вместо переменной х подставляем значение х₀=2.
Для этого в производную функции вместо переменной х подставляем значение х₀=2.
Для этого имеющиеся значения f(x₀), f'(x₀) и x₀ подставляем в вышеуказанную формулу уравнения касательной.
Для этого имеющиеся значения f(x₀), f'(x₀) и x₀ подставляем в вышеуказанную формулу уравнения нормали.
координаты фокусов:
длина осей : действительная ось 12; мнимая ось 10
эксцентриситет:
Пошаговое объяснение:
Каноническое уравнение гиперболы имеет вид
Приведем наше уравнение к каноническому виду.
900 переносим в правую часть и одновременно делим все части уравнения на 900.
Таким образом, мы получили каноническое уравнение гииперболы с центром в точке С(0; 0).
а = 6; b = 5
Действительная ось 2а = 12.
Мнимая ось 2b = 10
Расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: .
Фокусы имеют координаты F₁ (-c; 0) ; F₂(c; 0).
Найдем фокусы нашей гиперболы.
Эксцентриситетом гиперболы это отношение
#SPJ1
Написать уравнение касательной и нормали к графику функции f(x)=x^4/4-27x+60 в точке х₀=2.
ответ:Уравнение касательной имеет вид y=48-19x.
Уравнение нормали имеет вид y=188/19+х/19.
Пошаговое объяснение:Вспомним общий вид уравнения касательной:
И общий вид уравнения нормали:
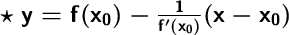
1. Найдём f(x₀).Для этого в функцию вместо переменной х подставляем значение х₀=2.
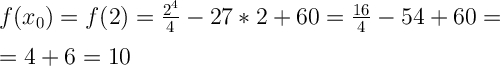
2. Найдём производную функции.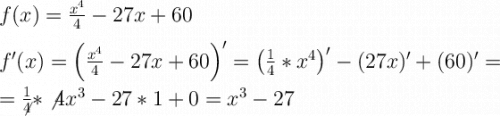
3. Найдём f'(x₀).Для этого в производную функции вместо переменной х подставляем значение х₀=2.
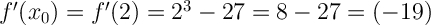
4. Записываем уравнение касательной.Для этого имеющиеся значения f(x₀), f'(x₀) и x₀ подставляем в вышеуказанную формулу уравнения касательной.
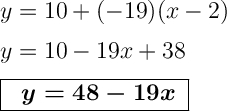
5. Записываем уравнение нормали.Для этого имеющиеся значения f(x₀), f'(x₀) и x₀ подставляем в вышеуказанную формулу уравнения нормали.
координаты фокусов:
длина осей : действительная ось 12; мнимая ось 10
эксцентриситет: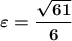
Пошаговое объяснение:
Каноническое уравнение гиперболы имеет вид
Приведем наше уравнение к каноническому виду.
900 переносим в правую часть и одновременно делим все части уравнения на 900.
Таким образом, мы получили каноническое уравнение гииперболы с центром в точке С(0; 0).
а = 6; b = 5
Действительная ось 2а = 12.
Мнимая ось 2b = 10
Расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: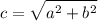 .
.
Фокусы имеют координаты F₁ (-c; 0) ; F₂(c; 0).
Найдем фокусы нашей гиперболы.
Эксцентриситетом гиперболы это отношение
#SPJ1