Більша основа трапеції вдвічі більша від меншої основи. Через точку перетину діагоналей проведено пряму, яка паралельна основам трапеції.  

Обчисли висоту отриманих трапецій, якщо висота даної трапеції дорівнює 21 см.

​

Биссектриса треугольника лежит между его высотой и медианой, которые проведены из той же вершины.

Поэтому K лежит на отрезке MH.

1.

Рассмотри ∠ACH и ∠ABC:

CA⊥BA и CH⊥BH по условию;

∠ACH = ∠ABC, как углы с взаимно перпендикулярными сторонами.

Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.

Поэтому CM = BM, тогда ΔBMC - равнобедренный.

Углы при основании равнобедренного треугольника равны.

Поэтому ∠MBC = ∠MCB, откуда ∠ACH = ∠MCB (т.к. ∠ACH = ∠MBC).

∠ACK = ∠BCK, как углы при биссектрисе;

∠ACH = ∠MCB;

Тогда ∠ACK - ∠ACH = ∠BCK - ∠MCB;

∠HCK = ∠MCK.

Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.

2.

Рассмотрим ΔMCH:

CK - биссектриса MCH, поскольку ∠HCK = ∠MCK;

Тогда справедливо равенство ;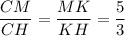

Пусть CM = 5x, тогда CH = 3x;

HM = HK+KM = 3+5 = 8;

ΔMCH - прямоугольный (CH⊥MH ⇒ ∠CHM = 90°);

Тогда по теореме Пифагора получим:

CH²+HM² = CM²;

(3x)²+8² = (5x)²;

9x²+64 = 25x²;

64 = 16x²;

x² = 64:16 = 2²;

x = 2.

CM = 5x = 5·2 = 10;

CH = 3x = 3·2 = 6.

3.

CM = BM = MA;

MA = 10;

AB = 2·MA = 2·10 = 20;

AH = MA-HM = 10-8 = 2.

4.

Рассмотрим ΔCHA:

∠CHA = 90°;  AH = 2;  CH = 6;

По теореме Пифагора найдём AC:

AC² = CH²+AH² = 6²+2² = 36+4 = 2²·10;

AC = 2√10.

5.

Рассмотрим ΔABC:

∠ACB = 90°;  AC = 10√2;  AB = 20;

По теореме Пифагора надём BC:

BC² = AB²-AC² = 20²-40 = 400-40 = 6²·10;

BC = 6√10.

6.

Рассмотрим ΔCHK:

∠CHK = 90°;  CH = 6;  HK = 3;

По теореме Пифагора найдём CK:

CK² = CH²+HK² = 6²+3² = 36+9 = 3²·5;

CK = 3√5.

ответ: AB = 20;  BC = 6√10;  AC = 2√10;  CK = 3√5.

Биссектриса треугольника лежит между его высотой и медианой, которые проведены из той же вершины.

Поэтому K лежит на отрезке MH.

1.

Рассмотри ∠ACH и ∠ABC:

CA⊥BA и CH⊥BH по условию;

∠ACH = ∠ABC, как углы с взаимно перпендикулярными сторонами.

Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.

Поэтому CM = BM, тогда ΔBMC - равнобедренный.

Углы при основании равнобедренного треугольника равны.

Поэтому ∠MBC = ∠MCB, откуда ∠ACH = ∠MCB (т.к. ∠ACH = ∠MBC).

∠ACK = ∠BCK, как углы при биссектрисе;

∠ACH = ∠MCB;

Тогда ∠ACK - ∠ACH = ∠BCK - ∠MCB;

∠HCK = ∠MCK.

Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.

2.

Рассмотрим ΔMCH:

CK - биссектриса MCH, поскольку ∠HCK = ∠MCK;

Тогда справедливо равенство ;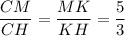

Пусть CM = 5x, тогда CH = 3x;

HM = HK+KM = 3+5 = 8;

ΔMCH - прямоугольный (CH⊥MH ⇒ ∠CHM = 90°);

Тогда по теореме Пифагора получим:

CH²+HM² = CM²;

(3x)²+8² = (5x)²;

9x²+64 = 25x²;

64 = 16x²;

x² = 64:16 = 2²;

x = 2.

CM = 5x = 5·2 = 10;

CH = 3x = 3·2 = 6.

3.

CM = BM = MA;

MA = 10;

AB = 2·MA = 2·10 = 20;

AH = MA-HM = 10-8 = 2.

4.

Рассмотрим ΔCHA:

∠CHA = 90°;  AH = 2;  CH = 6;

По теореме Пифагора найдём AC:

AC² = CH²+AH² = 6²+2² = 36+4 = 2²·10;

AC = 2√10.

5.

Рассмотрим ΔABC:

∠ACB = 90°;  AC = 10√2;  AB = 20;

По теореме Пифагора надём BC:

BC² = AB²-AC² = 20²-40 = 400-40 = 6²·10;

BC = 6√10.

6.

Рассмотрим ΔCHK:

∠CHK = 90°;  CH = 6;  HK = 3;

По теореме Пифагора найдём CK:

CK² = CH²+HK² = 6²+3² = 36+9 = 3²·5;

CK = 3√5.

ответ: AB = 20;  BC = 6√10;  AC = 2√10;  CK = 3√5.