Бабушке светы 60 лет. она старше отца светы .сейчас свете 10 лет . во сколько раз света моложе своего папы.? ​

200 м/мин = 200 · 60 : 1000 = 12 км/ч

Пусть х км/ч - скорость товарного поезда, тогда (х + 12) км/ч - скорость пассажирского поезда. Уравнение:

360/х - 360/(х+12) = 1

360 · (х + 12) - 360х = 1 · х · (х + 12)

360х + 4320 - 360х = х² + 12х

х² + 12х - 4320 = 0

D = b² - 4ac = 12² - 4 · 1 · (-4320) = 144 + 17280 = 17424

√D = √17424 = 132

х₁ = (-12-132)/(2·1) = (-144)/2 = -72 (не подходит, т.к. < 0)

х₂ = (-12+132)/(2·1) = 120/2 = 60

ответ: 60 км/ч.

Проверка:

360 : 60 = 6 ч - время движения товарного поезда

360 : (60+12) = 360 : 72 = 5 ч - время движения пассажирского поезда

6 - 5 = 1 ч - разница

x∈(0; +∞)

Пошаговое объяснение:

Одз:

x∈(-1; 0) ∪ (0; +∞)

1) При 0< X + 1 < 1 ⇒ -1 < x < 0;

получаем отрезок:

x∈(-1; 0) (1) он соответствует нашему ОДЗ, можно не вносить правки.

(2)

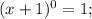Т.к , а единица всегда меньше 2. То выражение (2) не имеет решения.

2) При X+1 > 1 ⇒ X > 0

получаем отрезок:

x∈(0; +∞) Находим пересечение с ОДЗ, которые мы нашли ранее.

x∈(0; +∞) ∩ x∈(-1; 0) ∪ (0; +∞) = x∈(0; +∞) (3)

(4)

Т.к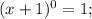 , а единица всегда меньше 2. То выражение (4) имеет бесконечное множества решений,  x∈(-∞; +∞). Найдя пересечения (3) и (4) :

x∈(0; +∞) ∩ x∈(-∞; +∞) = x∈(0; +∞)

Мы найдем отрезок удовлетворяющий всем условием задания

ответ: x∈(0; +∞)