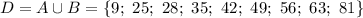Бассейн заполняется через 2 трубы за 10/3 часа. Если открыть одну первую трубу, то бассейн наполнится за 6 часов. За сколько времени наполнится бассейн через одну вторую трубу?

Відповідь:

У первого пирата до начала игры было 36 монет.

Покрокове пояснення:

Начнем с конца.

Вторая игра.) Второй пират проиграл половину своих монет (и отдал их первому). В результате после второй игры у первого оказалось 45 монет, а у второго оказалось 27 монет. Значит второй пират отдал первому 27 монет. До начала второй игры у первого пирата было 45 - 27 = 18 монет, а у второго пирата было 27 + 27 = 54 монеты.

Первая игра.) Первый пират проиграл половину своих монет (и отдал их второму). В результате после первой игры у первого пирата оказалось 18 монет, а у второго пирата оказалось 54 монеты. Значит первый пират отдал второму 18 монет. До начала первой игры у первого пирата было 18 + 18 = 36 монет, а у второго пирата было 54 - 18 = 36 монет.

Составим множество А. Выпишем нечётные натуральные числа из отрезка от 3 до 9:

3; 5; 7; 9

Теперь возведем их в квадрат:

9; 25; 49; 81

Значит:

Составим множество В. Выпишем целые числа из интервала от 3 до 10:

4; 5; 6; 7; 8; 9

Умножим их на 7:

28; 35; 42; 49; 56; 63

Значит:

Находим пересечение множеств А и В. В пересечение попадают элементы, принадлежащие одновременно и множеству А и множеству В:

Находим объединение множеств А и В. В объединение попадают элементы, принадлежащие хотя бы одному из множеств А или В: