Бесплатно за ответ вам ещё нужен​

1) 3/5 > 2/5.

2) 7/19 < 7/15.

3) 3/22 > 3/29.

4) 5/11 > 2/11.

5) 3/5 > 1/6.

Пошаговое объяснение:

1) 3/5 > 2/5.

Из двух дробей с равными знаменателями больше та, числитель которой больше.

3 > 2, 5=5, тогда 3/5 > 2/5.

2) 7/19 < 7/15.

Из двух дробей с равными числителями меньше та, знаменатель которой больше.

7=7, 19 > 15, тогда 7/19 < 7/15.

3) 3/22 > 3/29.

Из двух дробей с равными числителями больше та, знаменатель которой меньше.

3=3, 22 < 29, тогда 3/22 > 3/29.

4) 5/11 > 2/11.

Из двух дробей с равными знаменателями больше та, числитель которой больше.

5) 3/5 > 1/6.

3/5 > 3/18

Из двух дробей с равными числителями больше та, знаменатель которой меньше.

3=3, 5 < 18, тогда 3/5 > 3/18, т.е. 3/5 > 1/6.

Відповідь:

Покрокове пояснення:

а1 - проекція катета а на гіпотенузу

b1 - проекція катета b на гіпотенузу

a^2 = c*a1;   b^2 c*b

а)  c = 6 + 24 = 30 см

    a^2 = 30*6 = 180

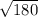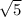    a = = 6 см

    b^2 = 30*24 = 720

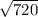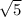    b = = 12 см

б)  c = 12 + 16 = 28

    a^2 = 28*12 = 336

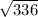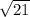    a = = 16 см

    b^2 = 28*16 = 448

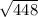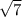    b = = 16 см

в)  c = 8 + 10 = 18 см

    a^2 = 18*8 = 144

    a =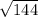 = 12 см

    b^2 = 18*10 = 180

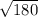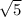    b = = 6 см

г)  c = 3 + 23 = 26

    a^2 = 26*3 = 78

    a =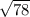 см

    b^2 = 26*23 = 598

    b =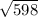 см