Систе́ма счисле́ния (англ. numeral system или system of numeration) — символический метод записи чисел, представление чисел с письменных знаков. Система счисления: даёт представления множества чисел (целых и/или вещественных); даёт каждому числу уникальное представление...
Системы Счисления бывают позиционные и непозиционные . На картинке выше символьная и римская СС являются хорошим примером непозиционной системы счисления. Как не переставляйте кружочки, смысл не поменяется их все равно будет десять.
В позиционной СС от позиции(разряда) цифры зависит ее значение. Например число 685 = 600(сотни) + 80(десятки) + 5(единицы), можно записать иначе 685 = 6 * 100 + 8 * 10 + 5 * 1. Если бы число 685 было непозиционным, то мы бы записали так, 685 = 6+8+5 = 19.
Для перевода числа из десятичной системы счисления в любую другую, необходимо это число разделить уголком на основание системы счисления. А в ответ записать остатки от деления в обратном порядке.
3628 если это число записано в десятичной системе то оно будет выглядеть так же.
в восьмеричной системе - будет выгладить( 3628 делим столбиком на 8 получаем 453 и 4 в остатке ) 4544
в шестнацатиричной - ( 3628 : 16 = 226 и 12 в остатке ) - 226С
Дано: 1) 1-ый возьмет 1 у второго и у него будет в 3 раза больше яблок; 2) 2-ой возьмет 1 яблоко у первого и будет поровну. Найти: сколько яблок у первого? Решение: 1 + 1 = 2 ябл. разница в яблоках 1-го и 2-го. Если первый передает яблоко второму, то у него будет на 1 меньше, а у второго на 1 больше, а т.к. сровнялись, то у первого было на 2 яблока больше. 2 + 1 + 1 = 4 ябл. будет разница между яблоками, когда второй отдаст 1 яблоко первому. 3 - 1 = 2 (части) будет разница в частях, т.к. у 1-го будет в три раза больше, значит 1 часть у второго и 3 части у первого. 4 ябл. = 2 части 4 : 2 = 2 (ябл) 1 часть будет у второго. (2+1=3 у него БЫЛО) 2 * 3 = 6 (ябл) будет у первого, когда возьмет 1 у второго 6 - 1 = 5 (ябл.) было у первого сначала. ответ: 5 яблок было у первого мальчика. Проверка: 5 - 1 = 3 + 1; 4 = 4
Пошаговое объяснение:
Систе́ма счисле́ния (англ. numeral system или system of numeration) — символический метод записи чисел, представление чисел с письменных знаков. Система счисления: даёт представления множества чисел (целых и/или вещественных); даёт каждому числу уникальное представление...
Системы Счисления бывают позиционные и непозиционные . На картинке выше символьная и римская СС являются хорошим примером непозиционной системы счисления. Как не переставляйте кружочки, смысл не поменяется их все равно будет десять.
В позиционной СС от позиции(разряда) цифры зависит ее значение. Например число 685 = 600(сотни) + 80(десятки) + 5(единицы), можно записать иначе 685 = 6 * 100 + 8 * 10 + 5 * 1. Если бы число 685 было непозиционным, то мы бы записали так, 685 = 6+8+5 = 19.
Для перевода числа из десятичной системы счисления в любую другую, необходимо это число разделить уголком на основание системы счисления. А в ответ записать остатки от деления в обратном порядке.
3628 если это число записано в десятичной системе то оно будет выглядеть так же.
в восьмеричной системе - будет выгладить( 3628 делим столбиком на 8 получаем 453 и 4 в остатке ) 4544
в шестнацатиричной - ( 3628 : 16 = 226 и 12 в остатке ) - 226С
в двоичной (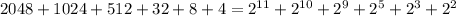
) = 1 1 1 0 0 0 1 0 1 1 0 0
а ты решай к какой СС отнести число 3628
2) 2-ой возьмет 1 яблоко у первого и будет поровну.
Найти: сколько яблок у первого?
Решение:
1 + 1 = 2 ябл. разница в яблоках 1-го и 2-го. Если первый передает яблоко второму, то у него будет на 1 меньше, а у второго на 1 больше, а т.к. сровнялись, то у первого было на 2 яблока больше.
2 + 1 + 1 = 4 ябл. будет разница между яблоками, когда второй отдаст 1 яблоко первому.
3 - 1 = 2 (части) будет разница в частях, т.к. у 1-го будет в три раза больше, значит 1 часть у второго и 3 части у первого.
4 ябл. = 2 части
4 : 2 = 2 (ябл) 1 часть будет у второго. (2+1=3 у него БЫЛО)
2 * 3 = 6 (ябл) будет у первого, когда возьмет 1 у второго
6 - 1 = 5 (ябл.) было у первого сначала.
ответ: 5 яблок было у первого мальчика.
Проверка: 5 - 1 = 3 + 1; 4 = 4