1. 1750 м/мин*2мин=3500м=3,5км - проезжает ока за 2 мин. 2. скорость БМВ в 2 раза выше скорости Оки
следовательно за это же время она преодолевает 3,5х2= 7 км - на этой отметке они встречаются. 3. 3,5 км *5=17,5 проезжает ока за 10 минут.
7 км*5=35 - проезжает БМВ т.к.за 2 мин.3,5 км, за 10 соотв. в 5 раз больше 4. 35 - 17,5= 17,5 км разница в расстоянии 5. 105 км/ч + 45 км/ч=150 км/ч -скорости после разворота а/м 6. 17,5 :150х60 =7 мин.
ответ: через 7 минут после разворота инспектор повстречает ОКУ
Ученики собрали 5590 г семян акации, дуба и клёна. Семян акации собрали в раза больше, чем клёна, а дуба - на 2550 г больше, чем акации. Сколько семян акации, дуба и клёна были собраны.
Допустим, что семян клёна собрали х грамм, семян акации 1,4х, семян дуба - (1,4х+2 550), тогда согласно этим данным можно составить уравнение:
1. 1750 м/мин*2мин=3500м=3,5км - проезжает ока за 2 мин.
2. скорость БМВ в 2 раза выше скорости Оки
следовательно за это же время она преодолевает 3,5х2= 7 км - на этой отметке они встречаются.
3. 3,5 км *5=17,5 проезжает ока за 10 минут.
7 км*5=35 - проезжает БМВ т.к.за 2 мин.3,5 км, за 10 соотв. в 5 раз больше
4. 35 - 17,5= 17,5 км разница в расстоянии
5. 105 км/ч + 45 км/ч=150 км/ч -скорости после разворота а/м
6. 17,5 :150х60 =7 мин.
ответ: через 7 минут после разворота инспектор повстречает ОКУ
Ученики собрали 5590 г семян акации, дуба и клёна. Семян акации собрали в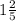 раза больше, чем клёна, а дуба - на 2550 г больше, чем акации. Сколько семян акации, дуба и клёна были собраны.
раза больше, чем клёна, а дуба - на 2550 г больше, чем акации. Сколько семян акации, дуба и клёна были собраны.
Допустим, что семян клёна собрали х грамм, семян акации 1,4х, семян дуба - (1,4х+2 550), тогда согласно этим данным можно составить уравнение:
х+1,4х+1,4х+2 550=5 590
3,8х+2552=5590
3,8х=5 590-2 550
3,8х=3 040
х=3 040:3,8
х=800 (г) - семена клёна.
1,4х=1,4·800=1 120 (г) - семена акации.
1,4х+2 550=1 120+2 550=3 670 (г) - семена дуба.
ответ: 800 грамм семена клёна, 1 120 грамм семена акации, 3 670 грамм семена дуба.