Пошаговое объяснение:
0 ; 1 ; 2 ... 2018 - возможные остатки от деления числа на 2019
( всего 2019 ) , пусть множество А состоит из различных чисел
вида 777...7 и количество элементов этого множества
больше чем 2019 , тогда найдутся 2 числа из А ,имеющие
одинаковые остатки при делении на 2019 , пусть это числа а
и b ; а > b ;a = 2019·n+r ; b = 2019·m+r , тогда а - b = 2019· t =
777...77...000...0 = 777...7 · ( количество цифр у
разности будет равно числу цифр числа а , причем число
нулей будет равно числу семерок у числа b ) , a - b кратно
2019 и равно произведению числа вида 777...7 и
, но числа 2019 и
взаимно простые ( нет общих делителей ) ⇒ 777...7 делится
нацело на 2019
а) Преобразуем сумму кубов: а³ + в³= (а+в)(а² - ав + в²).
а³ + в³= (а+в)(а² + 2ав + в² - 2ав - ав) = (а+в)(а + в)² - 3ав) =
= (а+в)³((а + в) - 3ав).
Для этого варианта х1 + х2 = -(-2)/0,5 = 4. х1 * х2 = (-5а + 1)/0,5 = -10а + 2.
Условие х1³ + х2³ < 40. Подставим: 4³ - 4*3*(-10а + 2) < 40,
64 + 120a - 24 < 40. Получаем а < 0.
Теперь надо определиться с пределом значения а, чтобы было два различных корня. Этот предел - когда дискриминант равен 0.
Д = в² - 4ас = 4 - 4*0,5(-5а + 1) = 4 + 10а - 2 = 0, а = -2/10 = -1/5 = -0,2.
ответ: -0,2< a < 0.
б) Решается аналогично.
Пошаговое объяснение:
0 ; 1 ; 2 ... 2018 - возможные остатки от деления числа на 2019
( всего 2019 ) , пусть множество А состоит из различных чисел
вида 777...7 и количество элементов этого множества
больше чем 2019 , тогда найдутся 2 числа из А ,имеющие
одинаковые остатки при делении на 2019 , пусть это числа а
и b ; а > b ;a = 2019·n+r ; b = 2019·m+r , тогда а - b = 2019· t =
777...77...000...0 = 777...7 ·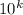
( количество цифр у
разности будет равно числу цифр числа а , причем число
нулей будет равно числу семерок у числа b ) , a - b кратно
2019 и равно произведению числа вида 777...7 и
взаимно простые ( нет общих делителей ) ⇒ 777...7 делится
нацело на 2019
а) Преобразуем сумму кубов: а³ + в³= (а+в)(а² - ав + в²).
а³ + в³= (а+в)(а² + 2ав + в² - 2ав - ав) = (а+в)(а + в)² - 3ав) =
= (а+в)³((а + в) - 3ав).
Для этого варианта х1 + х2 = -(-2)/0,5 = 4. х1 * х2 = (-5а + 1)/0,5 = -10а + 2.
Условие х1³ + х2³ < 40. Подставим: 4³ - 4*3*(-10а + 2) < 40,
64 + 120a - 24 < 40. Получаем а < 0.
Теперь надо определиться с пределом значения а, чтобы было два различных корня. Этот предел - когда дискриминант равен 0.
Д = в² - 4ас = 4 - 4*0,5(-5а + 1) = 4 + 10а - 2 = 0, а = -2/10 = -1/5 = -0,2.
ответ: -0,2< a < 0.
б) Решается аналогично.