Буклеты трех друзей. один день раздавал 598 буклетов, другой раздавал 736 буклетов, но третий не хотел раскрывать его. но оба друга быстро подсчитали, в общей сложности 1739 буклетов. каково было выступление третьего мальчика?
Пусть первая прямая имеет угловой коэффициент , а вторая прямая имеет угловой коэффициент , где и - соответствующие углы наклона прямых к положительному направлению оси .
Рассмотрим угол между этими прямыми. Пусть , тогда он равен . Найдем соотношение между этим углом и угловыми коэффициентами прямых. Используем формулу тангенса разности:
Так как мы хотим получить условие перпендикулярности двух прямых, то считаем угол между прямыми .
Тангенс 90 градусов не определен, но можно сказать что он стремится к бесконечности к стремлении аргумента к 90 градусам.
Но если дробь стремится к бесконечности, то знаменатель стремится к нулю.
В пределе знаменатель равен нулю. Тогда получим:
Можно выразить один из коэффициентов:
Тогда формулируется легкое правило: Две прямые перпендикулярны, когда их угловые коэффициенты являются противоположными обратными числами.
Пусть первая прямая имеет угловой коэффициент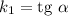 , а вторая прямая имеет угловой коэффициент
, а вторая прямая имеет угловой коэффициент 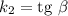 , где
, где 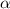 и
и 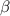 - соответствующие углы наклона прямых к положительному направлению оси
- соответствующие углы наклона прямых к положительному направлению оси 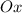 .
.
Рассмотрим угол между этими прямыми. Пусть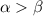 , тогда он равен
, тогда он равен  . Найдем соотношение между этим углом и угловыми коэффициентами прямых. Используем формулу тангенса разности:
. Найдем соотношение между этим углом и угловыми коэффициентами прямых. Используем формулу тангенса разности:
Так как мы хотим получить условие перпендикулярности двух прямых, то считаем угол между прямыми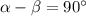 .
.
Тангенс 90 градусов не определен, но можно сказать что он стремится к бесконечности к стремлении аргумента к 90 градусам.
Но если дробь стремится к бесконечности, то знаменатель стремится к нулю.
В пределе знаменатель равен нулю. Тогда получим:
Можно выразить один из коэффициентов:
Тогда формулируется легкое правило: Две прямые перпендикулярны, когда их угловые коэффициенты являются противоположными обратными числами.
Доказательство теоремы Пифагора
Пусть треугольник ABC - прямоугольный треугольник с прямым углом C (рис. 2).
Проведём высоту из вершины C на гипотенузу AB, основание высоты обозначим как H .
Прямоугольный треугольник ACH подобен треугольнику ABC по двум углам ( ∠ACB=∠CHA=90∘, ∠A - общий). Аналогично, треугольник CBH подобен ABC .
Введя обозначения
BC=a,AC=b,AB=c
из подобия треугольников получаем, что
ac=HBa,bc=AHb
Отсюда имеем, что
a2=c⋅HB,b2=c⋅AH
Сложив полученные равенства, получаем
a2+b2=c⋅HB+c⋅AH
a2+b2=c⋅(HB+AH)
a2+b2=c⋅AB
a2+b2=c⋅c
a2+b2=c2
Что и требовалось доказать.