Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей Быстрей ​

можно применять в разной очередности эти две операции к числу 2017. В самом общем виде можно получить следующее:

(2^n)* 2017 - m(0)*17 - m(1)*2*17 - m(2)*(2^2)*17 - ... - m(n)*(2^n)*17

n и все m(k) - целые. Узнать, какой последовательностью действий получено число означает найти n и все m(k).

Обозначим полученное число: (2^n)*2017 - 17*S

S = m(0) + m(1)*2 + m(2)*(2^2) + ... + m(n)*(2^n) - это разложение по степеням двойки. Т.е. двоичная система счисления. Т.к. нет отрицательных степеней двойки, это разложение целого числа. Т.е. S - целое.

По условию:

2019 = (2^n)*2017 - 17*S

S = ( 2017*(2^n) - 2019)/17 = ( 2006 [ (2^n) - 1] + [ 11 * 2^n - 14 ] )/17 =

= 118 * ( 2^n - 1) + ( 11* 2^n - 13)/17

Ну теперь чтобы найти m(k), надо разложить S по степеням 2, т.е. записать в двоичной системе счисления. Если, конечно, найдутся такие целые n, при которых S - целое (при которых (11* 2^n - 13)/17 - целое ). Удачи :)

Числа A и B называются взаимно простыми, если НОД(А; В)=1.

Возможны различные варианты :

а) Если числа А и В простые, то НОД(А; В)=1. Например:

НОД(2; 3)=1, НОД(2; 5)=1, НОД(3; 7)=1.

1)

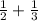
Так как НОД(2; 3)=1, то НОК(2; 3)=2·3=6

2)

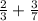
НОД(3; 7)=1, то НОК(3; 7)=3·7=21

б) Если числа А и В составные, но не имеют одинаковых простых делителей, тогда НОД(А; В)=1. Например:

НОД(4; 9)=1, НОД(4; 25)=1, НОД(9; 16)=1.

3)

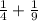
Так как НОД(4; 9)=1, то НОК(4; 9)=4·9=36

2)

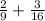
НОД(9; 16)=1, то НОК(9; 16)=9·16=144

В общем случае, если А и В взаимно простые, то есть

НОД(А; В)=1, то НОК(А; В)=А·В.