Поскольку при (другие "проблемные" точки начальной функции в промежуток, по которому берётся интеграл, не входят), то рассмотрим сходимость интеграла от эквивалентной функции.
Таким образом, поскольку интеграл от эквивалентной функции расходится на , то и изначальный тоже.
Поскольку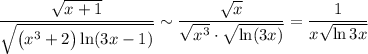
при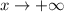 
(другие "проблемные" точки начальной функции в промежуток, по которому берётся интеграл, не входят), то рассмотрим сходимость интеграла от эквивалентной функции.
Таким образом, поскольку интеграл от эквивалентной функции расходится на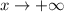
, то и изначальный тоже.
ответ.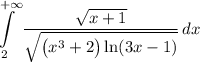
расходится