Здесь понадобится логарифмическое дифференцирование.
Сначала нужно прологарифмировать как левую, так и правую части:
Воспользуемся в правой части одним из свойств логарифма, из чего выйдет:
Теперь выражаем производную:
Здесь понадобится логарифмическое дифференцирование.
Сначала нужно прологарифмировать как левую, так и правую части:
Воспользуемся в правой части одним из свойств логарифма, из чего выйдет:
Теперь выражаем производную:
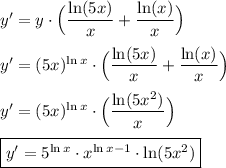
ответ: