Четыре точки были выбраны с поверхности сетки бумаги с квадратами, равными 1. Рассмотрим различные треугольники с тремя вершинами в этих точках и вычислим их площади. По крайней мере, что означает эта область?​

Задание № 2:

Сумма семи различных натуральных чисел равна 36. Наименьшее число равно 2. Назовите наибольшее число.

РЕШЕНИЕ: Возьмем последовательно семь натуральных чисел, начиная с 2, и найдем их сумму. 2+3+4+5+6+7+8=35. Так как до требуемой суммы не хватает всего 1, то нужно увеличить некоторое одно число на 1. Так как числа должны быть разными, то при увеличении любого числа, кроме последнего получим дублирующееся число. Значит, надо увеличить последнее число: 8+1=9 - это и есть наибольшее число.

ОТВЕТ: 9

MN=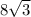 м

AO = 10 м

Пошаговое объяснение:

1# Достроим рисунок 39

У нас получился равнобедренный треугольник ΔKOM, так как KO=OM=R,поэтому:  KO=OM=R=8м (Значение радиуса взяли из выражения: R=KE+OL/2 )

Так как KO=OL=R ,то OL/2=OE = 4 м

Если OE = 4 м ,а OM=R=8м ,то найдём ME через теорему Пифагора:

м

Найдём MN:

MN=2*MN => MN=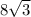 м

ответ: MN=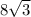 м

2# Достроим рисунок 40

    AB и СD - хорды ,и MN делит хорды пополам так:

AM=MB=6 м

СN=ND= 7 м

    Найдём у образованных треугольников ΔAMO и ΔCNO их гипотенузы через теорему Пифагора,которые и являются радиусами окружности:

Так как CO=AO=R ,то приравняем два выражения:

AM²+MO²=CN²+NO²

Обозначим ON=y ,то получается,что если MN=14 м,а тогда MO=14-y ,поэтому подставим все начения в уравнение:

6²+(14-y)²=8²+y²

Решаем уравнение и получаем:

y=6

Найдём MO:

MO=14-6=8 м

Теперь найдём через теорму Пифагора сам радиус AO :

м

ответ:  AO = 10 м