Числа F0, F1, F2,... заданы так: F0=0, F1=1, Fn+2=Fn+1+Fn для n=0,1,2 Докажите, что для каждого n большего или равного 0 подходит: Fn меньше/равно ((1+ корень из 5)/2)в степени n-1
Докажем тождество . Для этого заметим, что , что легко доказывается по индукции. Взяв определитель от обеих сторон, приходим к требуемому.
Теперь докажем лемму: для любого четного .
Доказательство: пусть . Сразу примем, что предел этой последовательности существует. Это равносильно .. Отсюда очевидно, что . Пусть . Тогда . Взяв предел от обеих частей, приходим к . Поскольку (применяя тождество, получаем разницу 1), лемма доказана.
Теперь по индукции.
База очевидна. Пусть для всех это верно. Докажем, что . Пусть четно, тогда , домножая на и применяя предположение индукции, получаем требуемое. Теперь неравенство выполняется для всех . Далее берем — четное число — и повторяем операцию. Тем самым докажем для всех нечетных чисел.
Теперь докажем для всех четных. , что и требовалось
Докажем тождество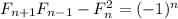 . Для этого заметим, что
. Для этого заметим, что ![\left[\begin{array}{cc}1&1\\1&0&\end{array}\right]^n= \left[\begin{array}{cc}F_{n+1}&F_{n}\\F{n}&F_{n-1}&\end{array}\right]](/tpl/images/1356/6491/4b6a3.png) , что легко доказывается по индукции. Взяв определитель от обеих сторон, приходим к требуемому.
, что легко доказывается по индукции. Взяв определитель от обеих сторон, приходим к требуемому.
Теперь докажем лемму: для любого четного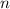
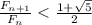 .
.
Доказательство: пусть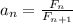 . Сразу примем, что предел этой последовательности существует. Это равносильно
. Сразу примем, что предел этой последовательности существует. Это равносильно 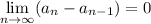 .
.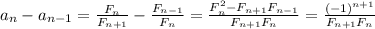 . Отсюда очевидно, что
. Отсюда очевидно, что 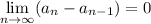 . Пусть
. Пусть 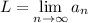 . Тогда
. Тогда 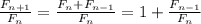 . Взяв предел от обеих частей, приходим к
. Взяв предел от обеих частей, приходим к 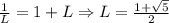 . Поскольку
. Поскольку 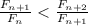 (применяя тождество, получаем разницу 1), лемма доказана.
(применяя тождество, получаем разницу 1), лемма доказана.
Теперь по индукции.
База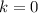 очевидна. Пусть для всех
очевидна. Пусть для всех 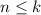 это верно. Докажем, что
это верно. Докажем, что 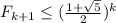 . Пусть
. Пусть 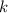 четно, тогда
четно, тогда 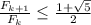 , домножая на
, домножая на 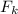 и применяя предположение индукции, получаем требуемое. Теперь неравенство выполняется для всех
и применяя предположение индукции, получаем требуемое. Теперь неравенство выполняется для всех 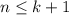 . Далее берем
. Далее берем 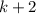 — четное число — и повторяем операцию. Тем самым докажем для всех нечетных чисел.
— четное число — и повторяем операцию. Тем самым докажем для всех нечетных чисел.
Теперь докажем для всех четных.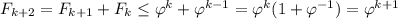 , что и требовалось
, что и требовалось