Точки, в которых функция точно неопределена: x1 = 2 Сначала находим производную: Применим правило производной частного:ddx(f(x)g(x))=1g2(x)(−f(x)ddxg(x)+g(x)ddxf(x))f(x)=x² и g(x)=x−2.Чтобы найти ddxf(x):В силу правила, применим: x² получим 2xЧтобы найти ddxg(x):дифференцируем x−2 почленно:Производная постоянной −2 равна нулю.В силу правила, применим: x получим 1В результате: 1Теперь применим правило производной деления:(1/(x−2)²)*(−x²+2x(x−2))Теперь упростим: ответ f'= x(x−4)/(x−2)².Экстремумы находим при f' = 0.Производная больше 0 - функция возрастает х∈(-00;0] U[4;00) убывает х∈[0;2)U[2;00)
№1. Найти значение выражения.
(8-6 1/4):(-5/8)-9×(-1/2-2/5)=
Разбиваем выражение по действиям(в первую очередь скобки,заткем деление, вычитание)
1) Первая скобка
8 - 6¹/₄ = 7⁴/₄-6¹/₄ = 1³/₄
2)Вторая скобка
- ¹/₂ - ²/₅ = - ⁵/₁₀ -⁴/₁₀ = - ⁹/₁₀
3) Деление первой скобки на (-5/8)
1³/₄ : (-⁵/₈) = ⁷/₄ ·(-⁸/₅) = -¹⁴/₅
4)Умножение второй скобки на 9
9· (-⁹/₁₀) = - ⁸¹/₁₀
5)Разность между 1 и 2 скобками
- ¹⁴/₅ - (-⁸¹/₁₀) = -²⁸/₁₀+ ⁸¹/₁₀= ⁵³/₁₀ = 5,3
ответ:5,3
№2. Решите задачу, составляя пропорцию.
За 0,4 кг конфет заплатили 75,6 р. Какова стоимость 0,3 кг этих конфет?
ПРОПОРЦИЯ:
за 0,4 кг - 75,6 руб.
За 0,3 кг - Х руб.
находим Х
Х=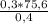
=56,7 руб.
ИЛИ составляем пропорцию так:
ответ: за 0,3 кг заплатили 56,7 руб
№3. Упростите выражение.
8(3х+5)-5×(2-9х)
Умножаем слагаемое из скобки на число,стоящее пеед скобкой:8*3х+5*8-5*2+5*9х
Знаки у множителей второй скобки поменялись на противоположные, тк. перед скобкой стоит знак "-"!
24х+40-10+45х
получаем ответ 30+69х
№4. Решите уравнение.
15х+12= 9х-6
слагаемые с "х" влево, остальные вправо. Следим за знаками(перенос с противоположными).
15х-9х=-6-12
6х=-18
х=-18/6
х=-3
Сначала находим производную:
Применим правило производной частного:ddx(f(x)g(x))=1g2(x)(−f(x)ddxg(x)+g(x)ddxf(x))f(x)=x² и g(x)=x−2.Чтобы найти ddxf(x):В силу правила, применим: x² получим 2xЧтобы найти ddxg(x):дифференцируем x−2 почленно:Производная постоянной −2 равна нулю.В силу правила, применим: x получим 1В результате: 1Теперь применим правило производной деления:(1/(x−2)²)*(−x²+2x(x−2))Теперь упростим: ответ f'= x(x−4)/(x−2)².Экстремумы находим при f' = 0.Производная больше 0 - функция возрастает х∈(-00;0] U[4;00) убывает х∈[0;2)U[2;00)