Составим таблицу 6х6 клеток. По диагонали таблицы ставим прочерки (-), т.к. команда не может играть сама с собой. Во все влетки ВЫШЕ диагонали ставим х - обозначение того, что команды сыграли между собой. Все клетки НИЖЕ диагонали повторяют клетки ВЫШЕ диагонали (игра команды 1 с командой 2 это то же самео, что и игра команды 2 с командой 1), поэтому их заполнять не будем. Следовательно, всего было сыграно столько матчей, сколько х в таблице (все клетки выше диагонали) - 15 матчей. Или (если считать снизу вверх) 1 + 2 + 3 + 4 + 5 = 15 матчей. Если команд было 7, то расчёт такой: 1 + 2 + 3 + 4 + 5 + 6 = 21 матч. Если команд n, то: 1 + 2 + 3 + ... + (n-3) + (n - 2) + (n - 1) =
Составим таблицу 6х6 клеток. По диагонали таблицы ставим прочерки (-), т.к. команда не может играть сама с собой. Во все влетки ВЫШЕ диагонали ставим х - обозначение того, что команды сыграли между собой. Все клетки НИЖЕ диагонали повторяют клетки ВЫШЕ диагонали (игра команды 1 с командой 2 это то же самео, что и игра команды 2 с командой 1), поэтому их заполнять не будем. Следовательно, всего было сыграно столько матчей, сколько х в таблице (все клетки выше диагонали) - 15 матчей. Или (если считать снизу вверх) 1 + 2 + 3 + 4 + 5 = 15 матчей. Если команд было 7, то расчёт такой: 1 + 2 + 3 + 4 + 5 + 6 = 21 матч. Если команд n, то: 1 + 2 + 3 + ... + (n-3) + (n - 2) + (n - 1) =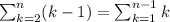
Пусть время движения по течению - x. 3 ч 45 минут = 3 3/4 часа = 15/4 часа.
Путь А-Б:
По течению туристы двигались со скоростью 30+2 = 32 км/ч. За время x со скоростью 32 км/ч они путь ≥ 56 км.
32x ≥ 56
x ≥ 56/32 = 7/4 = 1 ч 45 минут.
Путь Б-А:
ПРОТИВ течения туристы плыли (15/4 - x) часов со скоростью 30-2 = 28 км/ч, и путь ≥ 56 км.
(15/4 - x)28 ≥ 56
15/4 - x ≥ 2
-x ≥ -7/4
x ≤ 7/4 = 1 ч 45 минут
Так как неравенства x ≥ 7/4 и x ≤ 7/4 имеют разные знаки, то x = 7/4 (можно показать это на числовой прямой).