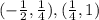Пошаговое объяснение:
Найдем точку пересечения сторон.
1) 3*x - 2*y = - 12
2) x - 3*y = - 11
Решаем систему уравнений методом Гаусса
3) 3*x -9*y = -33
Вычитаем 1) и 3)
4) 7*y = 21 и y = 21:3 = 7
Подставим в 2)
5) x = 3*y - 11 = 9 - 11 = -2
Точка А(-2;3) - вершина параллелограмма.
Находим уравнение малой диагонали АС.
ДАНО: А(-2;3), О(2;2)
1) k = ΔY/ΔX = (Аy-Оy)/(Аx-Оx)=(3-(2))/(-2-(2))=-0,25 - коэффициент наклона прямой
2) b=Аy-k*Аx=3-(-0,25)*-2=2,5- сдвиг по оси ОУ
Уравнение малой диагонали Y(АС) = -0,25*x+2,5 - ответ.
Находим положение вершины С - на таком же расстоянии АО от О.
Cx = Ox + (Ox- Ax) = 2 + (2-(-2)) = 6
Cy = Oy + (Oy- Ay) = 2 + (2-3) = 1
Вершина С(6;1).
Уравнения прямых приводим к канонической форме.
1) 3*x - 2*y + 12 = 0
2*y = 3*x + 12
y = 1.5*x + 6 - уравнение стороны АD.
2) x - 3*y + 11 = 0
3*y = x + 11
y = 1/3*x + 3 2/3 - уравнение стороны AВ.
Находим уравнение прямой ВС - параллельной AD
Дано: Точка C(6,1), наклон k = 1,5
b = Bу - k*Bx = 1 - (1,5)*(6) = -8
Уравнение стороны - прямой Y(BC) = 1,5*x - 8 - ответ
Находим вершину В - пересечение прямых АВ и СВ
1) х - 3*у = - 11
2) 1,5*х - у = 8
Опять методом Гаусса.
3) 1,5*х - 4,5 = - 16,5
Вычитаем 3) - 2)
4)3,5*у = 24,5
Cу = 24,5 : 3,5 = 7. Cх = 10, Вершина С(10;7).
Находим уравнение большой диагонали CD (CO)
ДАНО: C(10;7), О(2;2)
1) k = ΔY/ΔX = (Cy-Оy)/(Cx-Оx)=(7-(2))/(10-(2))= 5/8 (0,63) - коэффициент наклона прямой
2) b=Cy-k*Cx=7-(5/8)*10=0,75- сдвиг по оси ОУ
Уравнение Y(CО) = Y(CD)= 5/8*x + 0,75 - большая диагональ - ответ.
Находим уравнение стороны CD параллельной АВ.
Дано: Точка C(6,1), наклон k = 1/33
b = Cу - k*Cx = 1 - 1/3*6 = -1
Уравнение прямой - Y(CD) = 1/3*x - 1 - ответ
Рисунок с построением - в приложении.
Редкая и сложная задача - РЕШЕНА.
ответ: Увеличение на:
Убывает на: .
Пошаговое объяснение: Найдем производную.
Приравняем производную к 0.
Решим относительно x.
Упростим числитель.
Найдем НОЗ членов уравнения.
Умножим каждый член на и упростим.
Решим уравнение.
Разлагаем на множители левую часть уравнения.
Разделим обе части уравнения на 2. Результат деления 0 на любое ненулевое значение равен 0.
Приравняем x-1 к 0, затем решим относительно x.
Приравняем 2x+1 к 0, затем решим относительно x.
Решение является результатом x-1=0 и 2x+1=0.
Значения, которые обращают производную в 0 - 1, .
1, .
Выясним, при каких значениях переменной функция не определена.
Разобьем на интервалы вокруг значений x, в которых производная равна 0 или не определена.
Подставим значение из интервала в производную, чтобы определить, возрастает или убывает функция.
Увеличение на , так как .
Убывает на , поскольку
Подставим значение из интервала (0.25, 1) в производную, чтобы определить, возрастает или убывает функция.
Подставим значения из интервала в производную, чтобы определить, возрастает или убывает функция.
Перечислим промежутки, на которых функция возрастает и убывает.
Увеличение на:
Убывает на:
Пошаговое объяснение:
Найдем точку пересечения сторон.
1) 3*x - 2*y = - 12
2) x - 3*y = - 11
Решаем систему уравнений методом Гаусса
3) 3*x -9*y = -33
Вычитаем 1) и 3)
4) 7*y = 21 и y = 21:3 = 7
Подставим в 2)
5) x = 3*y - 11 = 9 - 11 = -2
Точка А(-2;3) - вершина параллелограмма.
Находим уравнение малой диагонали АС.
ДАНО: А(-2;3), О(2;2)
1) k = ΔY/ΔX = (Аy-Оy)/(Аx-Оx)=(3-(2))/(-2-(2))=-0,25 - коэффициент наклона прямой
2) b=Аy-k*Аx=3-(-0,25)*-2=2,5- сдвиг по оси ОУ
Уравнение малой диагонали Y(АС) = -0,25*x+2,5 - ответ.
Находим положение вершины С - на таком же расстоянии АО от О.
Cx = Ox + (Ox- Ax) = 2 + (2-(-2)) = 6
Cy = Oy + (Oy- Ay) = 2 + (2-3) = 1
Вершина С(6;1).
Уравнения прямых приводим к канонической форме.
1) 3*x - 2*y + 12 = 0
2*y = 3*x + 12
y = 1.5*x + 6 - уравнение стороны АD.
2) x - 3*y + 11 = 0
3*y = x + 11
y = 1/3*x + 3 2/3 - уравнение стороны AВ.
Находим уравнение прямой ВС - параллельной AD
Дано: Точка C(6,1), наклон k = 1,5
b = Bу - k*Bx = 1 - (1,5)*(6) = -8
Уравнение стороны - прямой Y(BC) = 1,5*x - 8 - ответ
Находим вершину В - пересечение прямых АВ и СВ
1) х - 3*у = - 11
2) 1,5*х - у = 8
Опять методом Гаусса.
3) 1,5*х - 4,5 = - 16,5
Вычитаем 3) - 2)
4)3,5*у = 24,5
Cу = 24,5 : 3,5 = 7. Cх = 10, Вершина С(10;7).
Находим уравнение большой диагонали CD (CO)
ДАНО: C(10;7), О(2;2)
1) k = ΔY/ΔX = (Cy-Оy)/(Cx-Оx)=(7-(2))/(10-(2))= 5/8 (0,63) - коэффициент наклона прямой
2) b=Cy-k*Cx=7-(5/8)*10=0,75- сдвиг по оси ОУ
Уравнение Y(CО) = Y(CD)= 5/8*x + 0,75 - большая диагональ - ответ.
Находим уравнение стороны CD параллельной АВ.
Дано: Точка C(6,1), наклон k = 1/33
b = Cу - k*Cx = 1 - 1/3*6 = -1
Уравнение прямой - Y(CD) = 1/3*x - 1 - ответ
Рисунок с построением - в приложении.
Редкая и сложная задача - РЕШЕНА.
ответ: Увеличение на: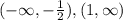
Убывает на: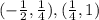 .
.
Пошаговое объяснение: Найдем производную.
Приравняем производную к 0.
Решим относительно x.
Упростим числитель.
Найдем НОЗ членов уравнения.
Умножим каждый член на и упростим.
и упростим.
Решим уравнение.
Разлагаем на множители левую часть уравнения.
Разделим обе части уравнения на 2. Результат деления 0 на любое ненулевое значение равен 0.
Приравняем x-1 к 0, затем решим относительно x.
Приравняем 2x+1 к 0, затем решим относительно x.
Решение является результатом x-1=0 и 2x+1=0.
Значения, которые обращают производную в 0 - 1,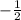 .
.
1,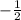 .
.
Выясним, при каких значениях переменной функция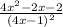 не определена.
не определена.
Разобьем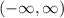 на интервалы вокруг значений x, в которых производная равна 0 или не определена.
на интервалы вокруг значений x, в которых производная равна 0 или не определена.
Подставим значение из интервала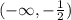 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на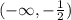 , так как
, так как 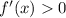 .
.
Подставим значение из интервала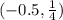 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Убывает на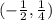 , поскольку
, поскольку 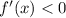
Подставим значение из интервала (0.25, 1) в производную, чтобы определить, возрастает или убывает функция.
Убывает на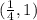 , поскольку
, поскольку 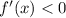
Подставим значения из интервала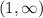 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на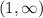 , так как
, так как 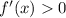 .
.
Перечислим промежутки, на которых функция возрастает и убывает.
Увеличение на: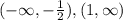
Убывает на: