Дан конус, у которого площадь боковой поверхности равна 65π см2, площадь полной поверхности равна 90π см2. Найди радиус основания, высоту, образующую, площадь основания и объём конуса.
Сначала распишем все формулы и тогда будем вычислять пошагово.
Формула площади боковой поверхности:
Формула площади полной поверхности:
Также формула площади полной поверхности: .
1) Площадь основания считается проще некуда, так как площадь полной поверхности - это сумма площади боковой поверхности и площади основания.
cм².
2) Отсюда считаем радиус основания:
. Радиус основания конуса равен 5 см.
3) Вычисляем образующую:
cм. Образующая равна 13 см.
4) Высоту вычислить ещё проще. Конус образуется вращением прямоугольного треугольника вокруг его катета (высоты). Высоту можно было бы вычислить по теореме Пифагора, но в этом нет необходимости, так как в данном случае присутствует египетский треугольник с катетами 5 см и 12 см и гипотенузой 13 см (в данном случае гипотенуза это образующая). Высота равна 12 см.
5) Объём конуса вычисляется по формуле:
В данном случае число мы трогать не будем, так как площади боковой и полной поверхностей представлены в форме с
Сначала распишем все формулы и тогда будем вычислять пошагово.
Формула площади боковой поверхности: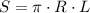
Формула площади полной поверхности: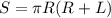
Также формула площади полной поверхности: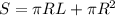 .
.
1) Площадь основания считается проще некуда, так как площадь полной поверхности - это сумма площади боковой поверхности и площади основания.
2) Отсюда считаем радиус основания:
3) Вычисляем образующую:
4) Высоту вычислить ещё проще. Конус образуется вращением прямоугольного треугольника вокруг его катета (высоты). Высоту можно было бы вычислить по теореме Пифагора, но в этом нет необходимости, так как в данном случае присутствует египетский треугольник с катетами 5 см и 12 см и гипотенузой 13 см (в данном случае гипотенуза это образующая). Высота равна 12 см.
5) Объём конуса вычисляется по формуле: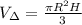
В данном случае число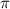 мы трогать не будем, так как площади боковой и полной поверхностей представлены в форме с
мы трогать не будем, так как площади боковой и полной поверхностей представлены в форме с