Вектор перпендикулярен плоскости основания и поэтому перпендикулярен любому вектору в этой плоскости, в частности AC.
Вектор BD перпендикулярен AC, поскольку в квадрате диагонали перпендикулярны. Поэтому вектор являющийся суммой векторов
и BD, также перпендикулярен AC.
Пошаговое объяснение:
Розглянемо трійку взаємно перпендикулярних одиничних векторів
AD = p , AB = q , AA₁ = r . Розкладемо вектори АС i DB₁ за цим базисом :
AC = p + q ; DB₁ = DA + AB + BB₁ = - p + q + r . Обчислимо скалярний добуток цих векторів :
AC * DB₁ = ( p + q ) * ( - p + q + r ) = - p² + p*q + p*r - p*q + q² + q*r =
= - 1² + 0 + 0 - 0 + 1² + 0 = 0 ( багато нулів , бо р ,q ,r перпендикулярні ) .
AC * DB₁ = 0 , тому вектори AC⊥ DB₁ . Отже , діагональ В₁D⊥AC .
Вектор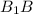
перпендикулярен плоскости основания и поэтому перпендикулярен любому вектору в этой плоскости, в частности AC.
Вектор BD перпендикулярен AC, поскольку в квадрате диагонали перпендикулярны. Поэтому вектор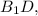
являющийся суммой векторов
Пошаговое объяснение:
Розглянемо трійку взаємно перпендикулярних одиничних векторів
AD = p , AB = q , AA₁ = r . Розкладемо вектори АС i DB₁ за цим базисом :
AC = p + q ; DB₁ = DA + AB + BB₁ = - p + q + r . Обчислимо скалярний добуток цих векторів :
AC * DB₁ = ( p + q ) * ( - p + q + r ) = - p² + p*q + p*r - p*q + q² + q*r =
= - 1² + 0 + 0 - 0 + 1² + 0 = 0 ( багато нулів , бо р ,q ,r перпендикулярні ) .
AC * DB₁ = 0 , тому вектори AC⊥ DB₁ . Отже , діагональ В₁D⊥AC .